Next: Biot-Savart Law Up: Magnetostatic Fields Previous: Charged Particle Motion in
Consider a thin, flat, uniform, ribbon of some conducting material that
is orientated such that its flat side is perpendicular to a uniform
magnetic field  . See Figure 2.19. Suppose that we pass a current
. See Figure 2.19. Suppose that we pass a current  along the length
of the ribbon. There are two alternatives. Either the current
is carried by positive charges
moving from left to right (in the figure),
or it is carried by negative charges moving in the opposite direction.
along the length
of the ribbon. There are two alternatives. Either the current
is carried by positive charges
moving from left to right (in the figure),
or it is carried by negative charges moving in the opposite direction.
Suppose that the
current is carried by positive charges moving from left to right.
These charges are deflected
upward (in the figure) by the magnetic field. Thus, the upper edge of the ribbon becomes
positively charged, while the lower edge becomes negatively charged.
Consequently, there is a positive potential difference 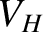 between the upper
and lower edges of the ribbon. This potential difference is called the Hall voltage.
between the upper
and lower edges of the ribbon. This potential difference is called the Hall voltage.
Suppose, now, that the current is carried by negative charges moving from right to left. These charges are also deflected upward by the magnetic field. Thus, the upper edge of the ribbon becomes negatively charged, while the lower edge becomes positively charged. It follows that the Hall voltage (i.e., the potential difference between the upper and lower edges of the ribbon) is negative in this case.
Clearly, it is possible to determine the sign of the mobile charges in a current-carrying conductor by measuring the Hall voltage. If the voltage is positive then the mobile charges are positive (assuming that the magnetic field and the current are orientated as shown in the figure), whereas if the voltage is negative then the mobile charges are negative. If we were to perform this experiment then we would discover that the mobile charges in metals are always negative (because they are electrons). However, in some types of semiconductor the mobile charges turn out to be positive. These positive charge carriers are called holes. Holes are actually missing electrons in the atomic lattice of the semiconductor, but they act essentially like positive charges.
Let us investigate the magnitude of the Hall voltage. Suppose that the mobile
charges each possess a charge  and move along the ribbon with the
drift velocity
and move along the ribbon with the
drift velocity 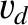 . The magnetic force on a given mobile charge
is of magnitude
. The magnetic force on a given mobile charge
is of magnitude 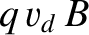 , because the charge moves essentially
perpendicular to the magnetic field. [See Equation (2.211).] In a steady state, this force
is balanced by the electric force due to the build up of charges
on the upper and lower edges of the ribbon. If the Hall voltage is
, because the charge moves essentially
perpendicular to the magnetic field. [See Equation (2.211).] In a steady state, this force
is balanced by the electric force due to the build up of charges
on the upper and lower edges of the ribbon. If the Hall voltage is
 , and the width of the ribbon is
, and the width of the ribbon is 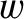 , then the electric
field directed from the upper to the lower edge of the ribbon is
of magnitude
, then the electric
field directed from the upper to the lower edge of the ribbon is
of magnitude  . [See Equation (2.17).] Now, the electric force on a mobile charge
is
. [See Equation (2.17).] Now, the electric force on a mobile charge
is  . [See Equation (2.10).] This force acts in opposition to the magnetic force.
In a steady state,
. [See Equation (2.10).] This force acts in opposition to the magnetic force.
In a steady state,
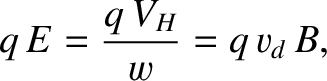 |
(2.222) |
Suppose that the thickness of the conducting ribbon is 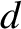 , and that it contains
, and that it contains
 mobile charge carriers per unit volume. It follows that the total current
flowing through the ribbon can be written
mobile charge carriers per unit volume. It follows that the total current
flowing through the ribbon can be written
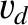 , width
, width
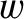 , and thickness
, and thickness 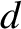 , flow past a given point on the ribbon in one second.
Combining Equations (2.223) and (2.224), we obtain
, flow past a given point on the ribbon in one second.
Combining Equations (2.223) and (2.224), we obtain
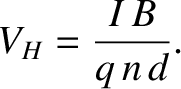 |
(2.225) |