Next: Lorentz Force Law Up: Magnetostatic Fields Previous: Magnetic Field
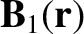 is generated by an electric current
is generated by an electric current 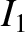 flowing through some circuit,
and a field
flowing through some circuit,
and a field
 is generated by a current
is generated by a current 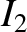 flowing through another
circuit, then when the currents
flowing through another
circuit, then when the currents 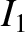 and
and 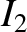 flow through both circuits
simultaneously the generated magnetic field is
flow through both circuits
simultaneously the generated magnetic field is
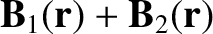 .
.
Consider two parallel wires separated by a perpendicular distance  ,
and carrying electric currents
,
and carrying electric currents 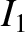 and
and 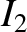 , respectively. The magnetic field-strength at the second wire due to the current flowing in the first wire
is
, respectively. The magnetic field-strength at the second wire due to the current flowing in the first wire
is
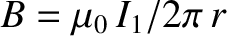 . [See Equation (2.206).] This field is orientated perpendicular to the second
wire, so the force per unit length exerted on the second wire is
. [See Equation (2.206).] This field is orientated perpendicular to the second
wire, so the force per unit length exerted on the second wire is
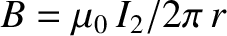 . This field
is orientated perpendicular to the first wire, so the force per unit length acting
on the first wire is equal and opposite to that acting on the second wire,
according to Equation (2.205). Equation (2.208) is known as Ampère's law.
. This field
is orientated perpendicular to the first wire, so the force per unit length acting
on the first wire is equal and opposite to that acting on the second wire,
according to Equation (2.205). Equation (2.208) is known as Ampère's law.
Equation (2.208) is the basis of the official (prior to 2019) SI definition of the ampere, which is:
One ampere is the magnitude of the current which, when flowing in each of two long parallel wires one meter apart, results in a force between the wires ofWe can see that it is no accident that the constantN per meter of length.
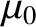 has the
numerical value of exactly
has the
numerical value of exactly
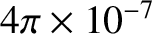 . (Incidentally, this rather strange definition arose because electromagnetism was originally formulated in the cgs system of units. In the cgs
system, the force per unit length exerted by two parallel wires, one centimeter apart,
both carrying a current of 1 abampere (i.e., 10 amperes), is
. (Incidentally, this rather strange definition arose because electromagnetism was originally formulated in the cgs system of units. In the cgs
system, the force per unit length exerted by two parallel wires, one centimeter apart,
both carrying a current of 1 abampere (i.e., 10 amperes), is 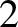 dynes per centimeter.)
dynes per centimeter.)