Energy Conservation
We have seen that the energy density of an electric field is given by
[see Equation (2.84)]
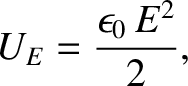 |
(2.546) |
whereas the energy density of a magnetic field takes the form
[see Equation (2.377)]
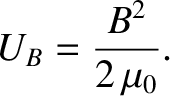 |
(2.547) |
This suggests that the energy density of a general electromagnetic field is
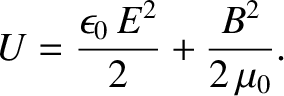 |
(2.548) |
Let us now demonstrate that Maxwell's equations conserve energy. We have already come across one conservation
law in electromagnetism; namely,
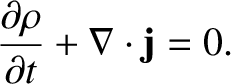 |
(2.549) |
(See Equation (2.473).]
The previous expression described the conservation of electric charge. Thus, integrating over some volume
 , bounded by a surface
, bounded by a surface  , and making use of the divergence theorem (see Section A.20), we obtain
, and making use of the divergence theorem (see Section A.20), we obtain
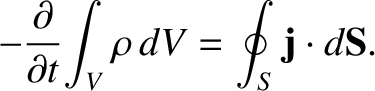 |
(2.550) |
In other words, the rate of decrease of the electric charge contained in volume  is equal to
the net flux of charge out of surface
is equal to
the net flux of charge out of surface  . This suggests that an energy conservation
law for electromagnetic fields should have the form
. This suggests that an energy conservation
law for electromagnetic fields should have the form
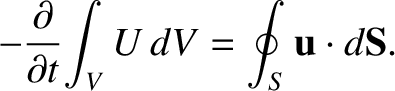 |
(2.551) |
Here,  is the energy density of the electromagnetic field, and
is the energy density of the electromagnetic field, and 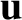 is
the flux of electromagnetic energy (i.e.,
energy
is
the flux of electromagnetic energy (i.e.,
energy  per unit time, per unit cross-sectional area, passes a given
point in the direction of
per unit time, per unit cross-sectional area, passes a given
point in the direction of 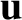 ). According to the previous equation, the
rate of decrease of the electromagnetic energy in volume
). According to the previous equation, the
rate of decrease of the electromagnetic energy in volume  is equal to the net flux
of electromagnetic energy out of surface
is equal to the net flux
of electromagnetic energy out of surface  .
.
Equation (2.551) is actually incomplete, because electromagnetic fields can gain or lose energy
by interacting with matter. We need to incorporate this fact into our analysis.
We saw earlier (see Section 2.1.11)
that the rate of heat dissipation per unit volume in a
conductor (the so-called ohmic heating rate) is
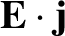 .
This energy is extracted from electromagnetic fields, so the rate of energy
loss of the fields in a volume
.
This energy is extracted from electromagnetic fields, so the rate of energy
loss of the fields in a volume  due to interaction with matter is
due to interaction with matter is
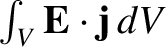 . Thus, Equation (2.551) generalizes to give
. Thus, Equation (2.551) generalizes to give
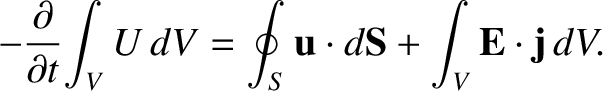 |
(2.552) |
From the divergence theorem (see Section A.20), the previous equation is equivalent to
 |
(2.553) |
Let us now see if we can derive an expression of this form from Maxwell's equations.
We start from the differential form of Ampère's law (including the displacement current), (2.487):
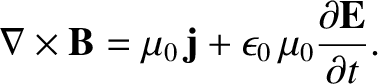 |
(2.554) |
The scalar product of the electric field with this equation yields
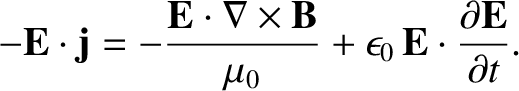 |
(2.555) |
The previous expression can be rewritten
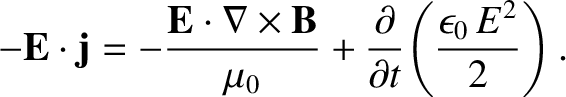 |
(2.556) |
However (see Section A.24),
 |
(2.557) |
so
 |
(2.558) |
The differential form of Faraday's law, (2.486), yields
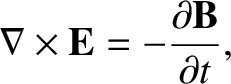 |
(2.559) |
so
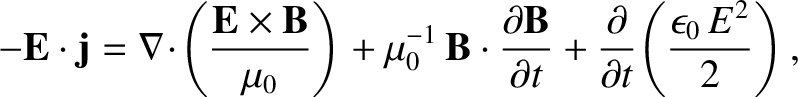 |
(2.560) |
which can be rewritten as
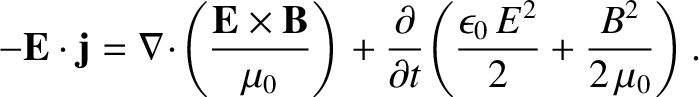 |
(2.561) |
Thus, we obtain the desired conservation law,
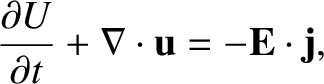 |
(2.562) |
where
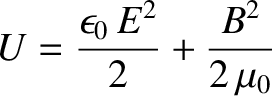 |
(2.563) |
is the electromagnetic energy density,
and
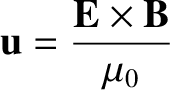 |
(2.564) |
is the electromagnetic energy flux. The latter quantity is usually called the
Poynting flux, after John Poynting who derived it in 1884.
Let us see whether our expression for the electromagnetic energy flux makes physical sense.
We know that if we stand in the Sun then we get hot. This
occurs because we absorb electromagnetic radiation emitted by the Sun. So,
radiation must transport energy. The electric and magnetic fields in electromagnetic
radiation are mutually perpendicular, and are also perpendicular to the direction
of propagation,
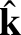 (which is a unit vector). Furthermore,
(which is a unit vector). Furthermore, 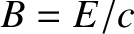 . (See Section 2.4.4.)
Equation (2.521) can easily be transformed into the following relation between
the electric and magnetic fields of an electromagnetic wave:
. (See Section 2.4.4.)
Equation (2.521) can easily be transformed into the following relation between
the electric and magnetic fields of an electromagnetic wave:
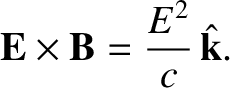 |
(2.565) |
Thus, the Poynting flux for electromagnetic radiation is
 |
(2.566) |
The previous expression states that electromagnetic waves transport energy along their
direction of propagation, which seems to make sense.
The energy density of electromagnetic radiation is
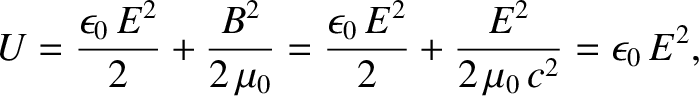 |
(2.567) |
where use has been made of  , and
, and
 . Note that
the electric and magnetic components of an electromagnetic wave have equal energy densities.
Because electromagnetic waves travel at the speed of light in vacuum, we would
expect the energy flux through one square meter in one second to equal the energy
contained in a volume of length
. Note that
the electric and magnetic components of an electromagnetic wave have equal energy densities.
Because electromagnetic waves travel at the speed of light in vacuum, we would
expect the energy flux through one square meter in one second to equal the energy
contained in a volume of length  , and unit cross-sectional area; that is,
, and unit cross-sectional area; that is,
 multiplied by the electromagnetic energy density. Thus,
multiplied by the electromagnetic energy density. Thus,
 |
(2.568) |
which is in accordance with the previous two equations.
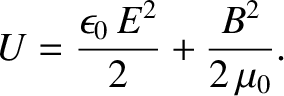
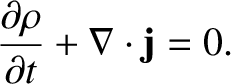
 , bounded by a surface
, bounded by a surface  , and making use of the divergence theorem (see Section A.20), we obtain
, and making use of the divergence theorem (see Section A.20), we obtain
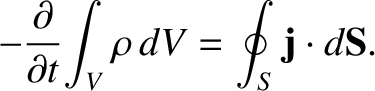
 is equal to
the net flux of charge out of surface
is equal to
the net flux of charge out of surface  . This suggests that an energy conservation
law for electromagnetic fields should have the form
Here,
. This suggests that an energy conservation
law for electromagnetic fields should have the form
Here,  is the energy density of the electromagnetic field, and
is the energy density of the electromagnetic field, and 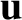 is
the flux of electromagnetic energy (i.e.,
energy
is
the flux of electromagnetic energy (i.e.,
energy  per unit time, per unit cross-sectional area, passes a given
point in the direction of
per unit time, per unit cross-sectional area, passes a given
point in the direction of 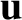 ). According to the previous equation, the
rate of decrease of the electromagnetic energy in volume
). According to the previous equation, the
rate of decrease of the electromagnetic energy in volume  is equal to the net flux
of electromagnetic energy out of surface
is equal to the net flux
of electromagnetic energy out of surface  .
.
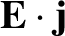 .
This energy is extracted from electromagnetic fields, so the rate of energy
loss of the fields in a volume
.
This energy is extracted from electromagnetic fields, so the rate of energy
loss of the fields in a volume  due to interaction with matter is
due to interaction with matter is
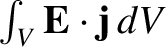 . Thus, Equation (2.551) generalizes to give
. Thus, Equation (2.551) generalizes to give
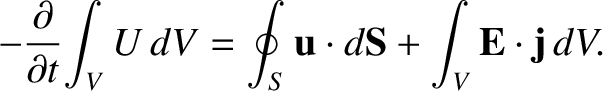



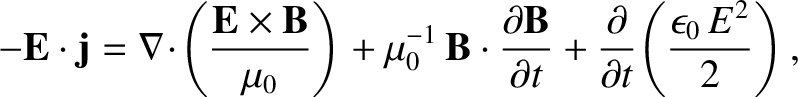
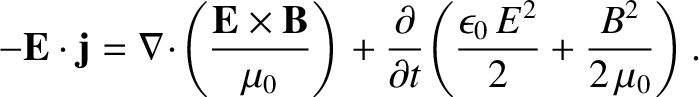
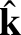 (which is a unit vector). Furthermore,
(which is a unit vector). Furthermore, 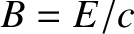 . (See Section 2.4.4.)
Equation (2.521) can easily be transformed into the following relation between
the electric and magnetic fields of an electromagnetic wave:
. (See Section 2.4.4.)
Equation (2.521) can easily be transformed into the following relation between
the electric and magnetic fields of an electromagnetic wave:
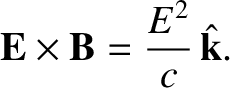
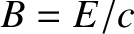 , and
, and
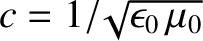 . Note that
the electric and magnetic components of an electromagnetic wave have equal energy densities.
Because electromagnetic waves travel at the speed of light in vacuum, we would
expect the energy flux through one square meter in one second to equal the energy
contained in a volume of length
. Note that
the electric and magnetic components of an electromagnetic wave have equal energy densities.
Because electromagnetic waves travel at the speed of light in vacuum, we would
expect the energy flux through one square meter in one second to equal the energy
contained in a volume of length  , and unit cross-sectional area; that is,
, and unit cross-sectional area; that is,
 multiplied by the electromagnetic energy density. Thus,
multiplied by the electromagnetic energy density. Thus,
