Next: Special Relativity Up: Maxwell's Equations Previous: Energy Conservation
 and length
and length
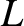 that is free
to move in one dimension. See Figure 2.42. Suppose that electromagnetic radiation of total
energy
that is free
to move in one dimension. See Figure 2.42. Suppose that electromagnetic radiation of total
energy  is emitted from one end of the car, propagates along the length of
the car, and is then absorbed at the other end. The effective mass of this radiation
is
is emitted from one end of the car, propagates along the length of
the car, and is then absorbed at the other end. The effective mass of this radiation
is 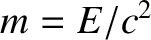 (from Einstein's famous relation
(from Einstein's famous relation 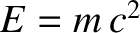 ). (See Section 3.3.4.) At first sight,
the process described previously appears to cause the center of mass of the system
to spontaneously shift. This violates the law of momentum conservation (assuming the
railway car is subject to no net horizontal external force). (See Section 1.4.4.) The only way in which the
center of mass of the system can remain stationary is if the railway car
moves in the opposite direction to the direction of propagation of
the radiation. In fact, if the car moves by a distance
). (See Section 3.3.4.) At first sight,
the process described previously appears to cause the center of mass of the system
to spontaneously shift. This violates the law of momentum conservation (assuming the
railway car is subject to no net horizontal external force). (See Section 1.4.4.) The only way in which the
center of mass of the system can remain stationary is if the railway car
moves in the opposite direction to the direction of propagation of
the radiation. In fact, if the car moves by a distance  then the center of
mass of the system is the same before and after the radiation pulse provided that
then the center of
mass of the system is the same before and after the radiation pulse provided that
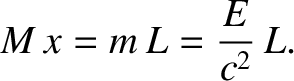 |
(2.569) |
 in this derivation.
in this derivation.
But, what actually causes the car to move? If the radiation possesses momentum,
 , then the car will recoil with the same momentum when the radiation is emitted.
When the radiation hits the other end of the car then the car acquires momentum
, then the car will recoil with the same momentum when the radiation is emitted.
When the radiation hits the other end of the car then the car acquires momentum
 in the opposite direction, which halts the motion. The time of flight of
the radiation is
in the opposite direction, which halts the motion. The time of flight of
the radiation is 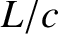 . So, the distance traveled by a mass
. So, the distance traveled by a mass  with momentum
with momentum
 in this time is
in this time is
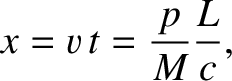 |
(2.570) |
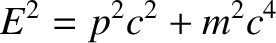 |
(2.572) |
 , momentum
, momentum  , and mass
, and mass  of a particle. (See Section 3.3.5.) According to
quantum theory, electromagnetic radiation is made up of massless particles
called photons. (See Section 3.3.8.) Thus,
of a particle. (See Section 3.3.5.) According to
quantum theory, electromagnetic radiation is made up of massless particles
called photons. (See Section 3.3.8.) Thus,
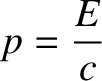 |
(2.573) |
It follows from Equation (2.571)
that the momentum density, 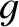 , of electromagnetic
radiation is equal to its energy density divided by
, of electromagnetic
radiation is equal to its energy density divided by  , so that
, so that
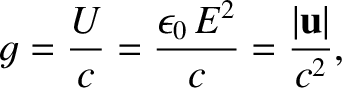 |
(2.574) |
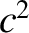 .
.
Of course, the electric field associated with an electromagnetic wave oscillates
rapidly in time, which implies that the previous expressions for the energy density,
energy flux, and momentum density of electromagnetic radiation also
oscillate rapidly. It is convenient to average over many periods of
the oscillation (this average is denoted
 ). Thus, from Equations (2.566), (2.567), and (2.575),
). Thus, from Equations (2.566), (2.567), and (2.575),
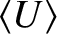 |
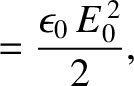 |
(2.576) |
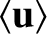 |
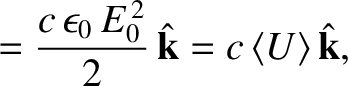 |
(2.577) |
 |
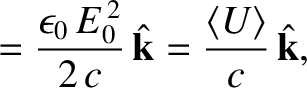 |
(2.578) |
 comes from averaging
comes from averaging
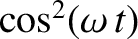 . Here,
. Here,
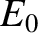 is the peak amplitude of the electric field associated with the wave.
is the peak amplitude of the electric field associated with the wave.
If electromagnetic radiation possesses momentum then it must exert a force on
bodies that absorb (or emit) radiation. Suppose that a body is placed in
a beam of perfectly collimated radiation, that it completely absorbs. The amount
of momentum absorbed per unit time, per unit cross-sectional area, is simply the
amount of momentum contained in a volume of length  , and unit cross-sectional
area; that is,
, and unit cross-sectional
area; that is,  multiplied by the momentum density,
multiplied by the momentum density, 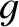 . An absorbed momentum per
unit time, per unit area, is equivalent to a pressure. In other words, the radiation
exerts a pressure
. An absorbed momentum per
unit time, per unit area, is equivalent to a pressure. In other words, the radiation
exerts a pressure  on the body. Thus, the radiation pressure is given by
on the body. Thus, the radiation pressure is given by
Consider a cavity filled with electromagnetic radiation. What is the radiation
pressure exerted on the walls? In this situation, the radiation propagates in
all directions with equal probability. Consider radiation propagating at an
angle  to the local normal to the wall. The amount of such radiation
hitting the wall per unit time, per unit area, is proportional to
to the local normal to the wall. The amount of such radiation
hitting the wall per unit time, per unit area, is proportional to
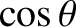 .
Moreover, the component of momentum normal to the wall that the radiation
carries is also proportional to
.
Moreover, the component of momentum normal to the wall that the radiation
carries is also proportional to
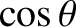 . Thus, the pressure exerted on the
wall is the same as in Equation (2.579), except that it is weighted by the
average of
. Thus, the pressure exerted on the
wall is the same as in Equation (2.579), except that it is weighted by the
average of
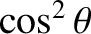 over all solid angles, in order to take into account
the fact
that obliquely propagating radiation exerts a pressure that is
over all solid angles, in order to take into account
the fact
that obliquely propagating radiation exerts a pressure that is
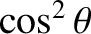 times that of normal radiation. The average of
times that of normal radiation. The average of
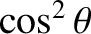 over all solid angles
is
over all solid angles
is 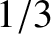 , so for isotropic radiation
, so for isotropic radiation
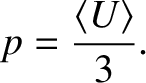 |
(2.580) |
The power incident on the surface of the Earth, due to radiation emitted by
the Sun, is about 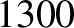 W m
W m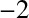 . So, what is the radiation pressure?
Because,
. So, what is the radiation pressure?
Because,
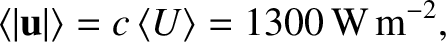 |
(2.581) |
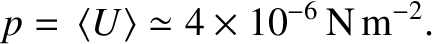 |
(2.582) |
 N m
N m ). Nevertheless, this small pressure due to
radiation is important in outer space, because it
is responsible for continuously sweeping
dust particles out of the solar system. It is quite common for comets to exhibit
two separate tails. One, known as the gas tail, consists of ionized gas, and is
swept along by the solar wind (a stream of charged particles and magnetic field-lines
emitted by the Sun). The other, known as the dust tail, consists of uncharged
dust particles, and is swept radially outward (because light travels in straight-lines) from the Sun by radiation pressure.
Two separate
tails are observed if the local direction of the solar wind is not radially
outward from the Sun (which is quite often the case).
). Nevertheless, this small pressure due to
radiation is important in outer space, because it
is responsible for continuously sweeping
dust particles out of the solar system. It is quite common for comets to exhibit
two separate tails. One, known as the gas tail, consists of ionized gas, and is
swept along by the solar wind (a stream of charged particles and magnetic field-lines
emitted by the Sun). The other, known as the dust tail, consists of uncharged
dust particles, and is swept radially outward (because light travels in straight-lines) from the Sun by radiation pressure.
Two separate
tails are observed if the local direction of the solar wind is not radially
outward from the Sun (which is quite often the case).
The radiation pressure from sunlight is very weak. However, that produced by
laser beams can be enormous (far higher than any conventional pressure which
has ever been produced in a laboratory). For instance, the lasers used in inertial confinement fusion (e.g., the National Ignition Facility at
Lawrence Livermore National Laboratory)
typically have energy fluxes of 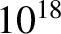 W m
W m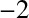 .
This translates to a radiation pressure of about
.
This translates to a radiation pressure of about 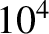 atmospheres.
atmospheres.