Next: Relativistic Doppler Effect Up: Relativistic Dynamics Previous: Relativistic Momentum Conservation
 , according to
where
, according to
where  is Planck's constant divided by
is Planck's constant divided by 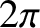 . (See Section 4.1.2.) However, we also know that a photon travels at the
speed of light in all inertial reference frames. Thus, the relativistic energy, (3.177), of a photon can
only be finite if the photon is a massless particle. In other words, a photon's rest mass must be zero.
Hence, the previous two equations suggest that the momentum of a photon has the magnitude
But, the dispersion relation of electromagnetic radiation in a vacuum, and, hence, of a photon moving through a
vacuum, is
Here,
. (See Section 4.1.2.) However, we also know that a photon travels at the
speed of light in all inertial reference frames. Thus, the relativistic energy, (3.177), of a photon can
only be finite if the photon is a massless particle. In other words, a photon's rest mass must be zero.
Hence, the previous two equations suggest that the momentum of a photon has the magnitude
But, the dispersion relation of electromagnetic radiation in a vacuum, and, hence, of a photon moving through a
vacuum, is
Here,  is the wavevector of the radiation, and, hence, of the photon. Note that the direction of
is the wavevector of the radiation, and, hence, of the photon. Note that the direction of  corresponds to the direction of motion of the photon. It is, thus, plausible that the momentum of our photon
is written
corresponds to the direction of motion of the photon. It is, thus, plausible that the momentum of our photon
is written
Consider the two inertial reference frames,  and
and  , discussed in the Section 3.3.6. Let
, discussed in the Section 3.3.6. Let  and
and  be the angular frequency and wavevector, respectively, of our photon in
be the angular frequency and wavevector, respectively, of our photon in  . Likewise, let
. Likewise, let 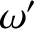 and
and  be the angular frequency and wavevector, respectively, of our photon in
be the angular frequency and wavevector, respectively, of our photon in  . Equations (3.180)–(3.183),
(3.197), and (3.200)
suggest that
. Equations (3.180)–(3.183),
(3.197), and (3.200)
suggest that