Next: Transverse Doppler Effect Up: Relativistic Dynamics Previous: Photons
 and
and  , discussed in Section 3.3.6.
Suppose that we place a radiation source at the origin of reference frame
, discussed in Section 3.3.6.
Suppose that we place a radiation source at the origin of reference frame  . Let the source emit plane waves of
angular frequency
. Let the source emit plane waves of
angular frequency  that travel in the positive
that travel in the positive  -direction. It follows that the wavevector of the
radiation in
-direction. It follows that the wavevector of the
radiation in  is
is
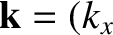 , 0, 0), where
[See Equation (3.199).]
, 0, 0), where
[See Equation (3.199).]
Consider an observer located at the origin
of frame  . To this observer, the radiation source appears to move at the speed
. To this observer, the radiation source appears to move at the speed
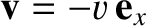 .
Let
.
Let
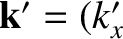 , 0, 0) and
, 0, 0) and 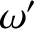 be the wavevector and angular frequency of the radiation
measured by our observer. It follows from Equations (3.201), (3.204), and (3.205) that
be the wavevector and angular frequency of the radiation
measured by our observer. It follows from Equations (3.201), (3.204), and (3.205) that
 |
 |
(3.206) |
 |
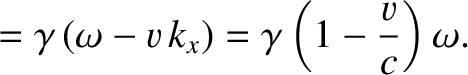 |
(3.207) |
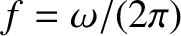 and
and
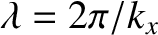 be the frequency (in hertz) and wavelength, respectively, of the
radiation emitted by the source in its rest frame, and let
be the frequency (in hertz) and wavelength, respectively, of the
radiation emitted by the source in its rest frame, and let
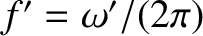 and
and
 be the frequency (in hertz) and wavelength, respectively, of the
radiation measured by an observer in the frame
be the frequency (in hertz) and wavelength, respectively, of the
radiation measured by an observer in the frame  , in which the source recedes directly away from the observer at the speed
, in which the source recedes directly away from the observer at the speed  .
Given that
.
Given that
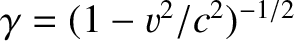 , we deduce that
It follows that if a radiation source recedes from an observer (or vice versa, because, in the absence of a medium through which electromagnetic waves propagate, all motion of sources and observers is relative) then the wavelength and frequency of the radiation
measured by the observer will be larger and smaller, respectively, than the corresponding values measured in the rest frame of the source. This shift in the wavelength and frequency of electromagnetic radiation due to the relative motion of the
observer and source is known as the relativistic Doppler effect. [Note that the non-relativistic Doppler effect for
sound waves takes a different form to Equations (3.208) and (3.209) because motion of the source and the observer can
be distinguished from one another in the presence of a medium though which the waves travel.]
, we deduce that
It follows that if a radiation source recedes from an observer (or vice versa, because, in the absence of a medium through which electromagnetic waves propagate, all motion of sources and observers is relative) then the wavelength and frequency of the radiation
measured by the observer will be larger and smaller, respectively, than the corresponding values measured in the rest frame of the source. This shift in the wavelength and frequency of electromagnetic radiation due to the relative motion of the
observer and source is known as the relativistic Doppler effect. [Note that the non-relativistic Doppler effect for
sound waves takes a different form to Equations (3.208) and (3.209) because motion of the source and the observer can
be distinguished from one another in the presence of a medium though which the waves travel.]
By analogy with the previous two formulae, if the source moves directly toward the observer with the speed  then
then
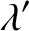 |
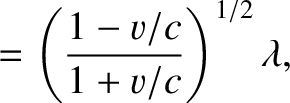 |
(3.210) |
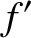 |
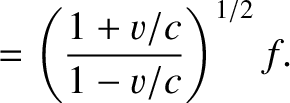 |
(3.211) |
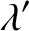 |
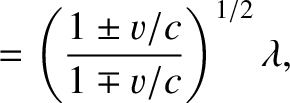 |
(3.212) |
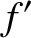 |
 |
(3.213) |