Next: Relativistic Momentum Conservation Up: Relativistic Dynamics Previous: Relativistic Energy-Momentum Relation
 and
and  . Let
. Let  move with velocity
move with velocity
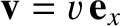 , and be in a standard configuration, with respect to
, and be in a standard configuration, with respect to  . Let
. Let  and
and  be some particle's momentum and energy, respectively, in
be some particle's momentum and energy, respectively, in  . Likewise,
let
. Likewise,
let 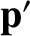 and
and 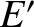 be the particle's momentum and energy, respectively, in
be the particle's momentum and energy, respectively, in  . We have seen that the transformation of
spacetime coordinates, (3.110)–(3.113), implies that the spacetime interval,
. We have seen that the transformation of
spacetime coordinates, (3.110)–(3.113), implies that the spacetime interval,
 , takes the
same value in all inertial frames of reference.
Given that
, takes the
same value in all inertial frames of reference.
Given that
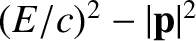 also takes the same value in all inertial frames of reference, it seems reasonable to assume, by analogy, that the components of
also takes the same value in all inertial frames of reference, it seems reasonable to assume, by analogy, that the components of  and
and  in our two inertial
reference frames are related as follows:
in our two inertial
reference frames are related as follows:
We can easily test out the previous transformation rule. Suppose that the particle is at rest in  . It follows
that
. It follows
that
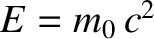 and
and
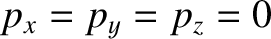 . Hence, Equations (3.180)–(3.183) yield
. Hence, Equations (3.180)–(3.183) yield
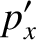 |
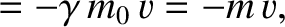 |
(3.184) |
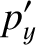 |
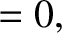 |
(3.185) |
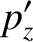 |
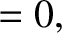 |
(3.186) |
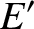 |
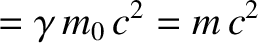 |
(3.187) |
 .
In other words, in the frame
.
In other words, in the frame  , in which the particle moves with velocity
, in which the particle moves with velocity 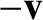 , we have
, we have
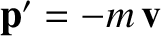 and
and 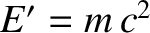 . Of course, these are the correct results. (See Sections 3.3.2
and 3.3.4.)
. Of course, these are the correct results. (See Sections 3.3.2
and 3.3.4.)