Relativistic Equation of Motion
Suppose that the particle discussed in the previous section has a mass 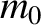 in its instantaneous rest frame.
Given that the particle's acceleration in its instantaneous rest frame is
in its instantaneous rest frame.
Given that the particle's acceleration in its instantaneous rest frame is
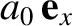 , the particle is clearly subject to a
force
, the particle is clearly subject to a
force
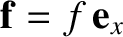 , where
, where
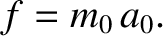 |
(3.158) |
Thus, according to Equation (3.153), the particle's equation of motion in an inertial
reference frame in which its instantaneous velocity is
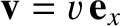 is
is
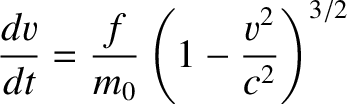 |
(3.159) |
However, the previous equation can be rearranged to give
![$\displaystyle f = \frac{d}{dt}\!\left[\frac{m_0\,v}{(1-v^2/c^2)^{1/2}}\right] = \frac{d(\gamma\,m_0\,v)}{dt}.$](img2594.png) |
(3.160) |
Let us define the relativistic mass of the particle as
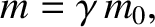 |
(3.161) |
and its relativistic momentum as
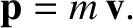 |
(3.162) |
Thus, Equation (3.160) implies that the relativistic equation of motion of the
particle is
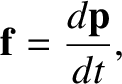 |
(3.163) |
which is analogous in form to Newton's second law of motion, (1.17). Thus, we
conclude that the reason that a particle of rest mass (i.e., mass in its instantaneous
rest frame) 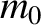 , subject to a constant force
, subject to a constant force 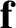 , never achieves a speed greater than
the speed of light is that the particle's relativistic mass,
, never achieves a speed greater than
the speed of light is that the particle's relativistic mass,
 , increases as it moves faster, and tends to infinity as
its speed approaches the speed of light.
, increases as it moves faster, and tends to infinity as
its speed approaches the speed of light.
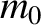 in its instantaneous rest frame.
Given that the particle's acceleration in its instantaneous rest frame is
in its instantaneous rest frame.
Given that the particle's acceleration in its instantaneous rest frame is
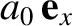 , the particle is clearly subject to a
force
, the particle is clearly subject to a
force
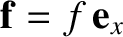 , where
, where
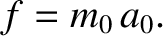
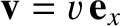 is
is
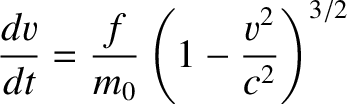
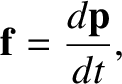
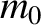 , subject to a constant force
, subject to a constant force 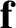 , never achieves a speed greater than
the speed of light is that the particle's relativistic mass,
, never achieves a speed greater than
the speed of light is that the particle's relativistic mass,
 , increases as it moves faster, and tends to infinity as
its speed approaches the speed of light.
, increases as it moves faster, and tends to infinity as
its speed approaches the speed of light.