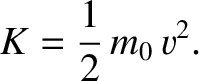Suppose that the force
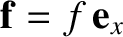 , that acts on the particle discussed in the previous section, causes
the particle to displace a distance
, that acts on the particle discussed in the previous section, causes
the particle to displace a distance
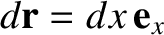 . The net work done on the particle is clearly
. The net work done on the particle is clearly
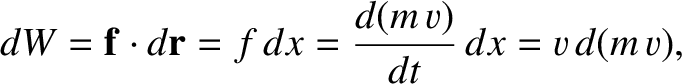 |
(3.164) |
because, by definition, 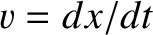 . (See Section 1.3.2.)
Here, use has been made of Equations (3.160) and (3.161).
However,
. (See Section 1.3.2.)
Here, use has been made of Equations (3.160) and (3.161).
However,
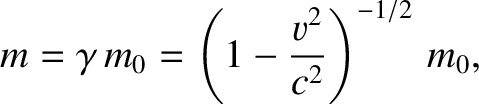 |
(3.165) |
so
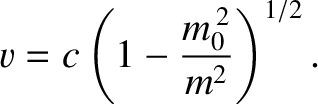 |
(3.166) |
The previous equation can be combined with Equation (3.164) to give
Suppose that the particle is initially at rest, so that its initial relativistic mass is 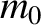 . Let the
force perform net work
. Let the
force perform net work 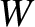 on the particle, in the process causing its relativistic mass to increase to
on the particle, in the process causing its relativistic mass to increase to  .
It is clear from the previous equation that
.
It is clear from the previous equation that
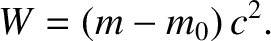 |
(3.168) |
However, we know that the net work that a force does on a particle causes the particle's kinetic energy, 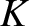 , to increase by a corresponding amount. (See Section 1.3.2.)
Thus, given that the particle's initial kinetic energy is zero, we deduce that its kinetic energy is
, to increase by a corresponding amount. (See Section 1.3.2.)
Thus, given that the particle's initial kinetic energy is zero, we deduce that its kinetic energy is
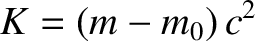 |
(3.169) |
when its relativistic mass is  .
.
Equation (3.169) can be combined with Equation (3.165) to give
![$\displaystyle K = m_0\,c^2\left[\left(1-\frac{v^2}{c^2}\right)^{-1/2}-1\right].$](img2611.png) |
(3.170) |
In the limit that the particle is moving at a non-relativistic speed, such that 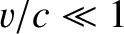 , the previous equation
reduces to
, the previous equation
reduces to
![$\displaystyle K \simeq m_0\,c^2\left[\left(1+ \frac{1}{2}\,\frac{v^2}{c^2}+\cdots\right)-1\right],$](img2612.png) |
(3.171) |
or
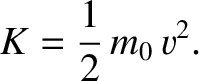 |
(3.172) |
This is consistent with the Newtonian definition of kinetic energy, as long as we identify the
rest mass of the particle with its mass in Newtonian dynamics. (See Section 1.3.2.)
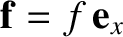 , that acts on the particle discussed in the previous section, causes
the particle to displace a distance
, that acts on the particle discussed in the previous section, causes
the particle to displace a distance
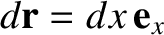 . The net work done on the particle is clearly
because, by definition,
. The net work done on the particle is clearly
because, by definition, 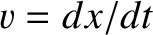 . (See Section 1.3.2.)
Here, use has been made of Equations (3.160) and (3.161).
However,
so
. (See Section 1.3.2.)
Here, use has been made of Equations (3.160) and (3.161).
However,
so
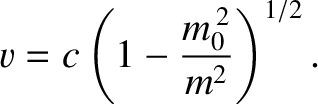
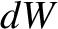
![$\displaystyle = c^2\left(1-\frac{m_0^{\,2}}{m^2}\right)^{1/2}d\!\left[m\left(1-\frac{m_0^{\,2}}{m^2}\right)^{1/2}\right]$](img2604.png)
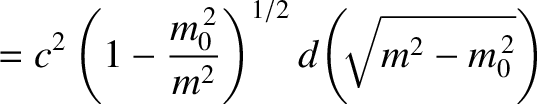
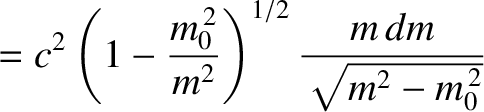
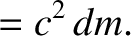
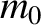 . Let the
force perform net work
. Let the
force perform net work 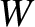 on the particle, in the process causing its relativistic mass to increase to
on the particle, in the process causing its relativistic mass to increase to  .
It is clear from the previous equation that
.
It is clear from the previous equation that
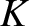 , to increase by a corresponding amount. (See Section 1.3.2.)
Thus, given that the particle's initial kinetic energy is zero, we deduce that its kinetic energy is
when its relativistic mass is
, to increase by a corresponding amount. (See Section 1.3.2.)
Thus, given that the particle's initial kinetic energy is zero, we deduce that its kinetic energy is
when its relativistic mass is  .
.
![$\displaystyle K = m_0\,c^2\left[\left(1-\frac{v^2}{c^2}\right)^{-1/2}-1\right].$](img2611.png)
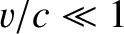 , the previous equation
reduces to
, the previous equation
reduces to
![$\displaystyle K \simeq m_0\,c^2\left[\left(1+ \frac{1}{2}\,\frac{v^2}{c^2}+\cdots\right)-1\right],$](img2612.png)