Consider a particle that moves with constant acceleration
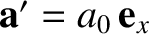 in
its instantaneous rest frame,
in
its instantaneous rest frame,  . Let the particle be located at the origin of
. Let the particle be located at the origin of  at time
at time 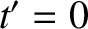 . It follows that a very short time,
. It follows that a very short time,
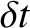 , later, the particle's spacetime coordinates in
, later, the particle's spacetime coordinates in  are
Consider a second frame of reference,
are
Consider a second frame of reference,  , that moves with velocity -
, that moves with velocity -
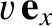 with respect to
with respect to  , and is also in a standard configuration with respect to
, and is also in a standard configuration with respect to  .
Thus, the particle's instantaneous velocity in
.
Thus, the particle's instantaneous velocity in  is
is
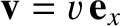 . In
. In  , the particle moves from the origin at time
, the particle moves from the origin at time  , to a point whose spacetime coordinates are
where
, to a point whose spacetime coordinates are
where
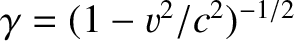 ,
a very short time later. Here, use has been made of Equations (3.104)–(3.107), as well as Equations (3.139)–(3.142). If
,
a very short time later. Here, use has been made of Equations (3.104)–(3.107), as well as Equations (3.139)–(3.142). If
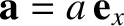 is the particle's instantaneous acceleration in
is the particle's instantaneous acceleration in
 then we expect the relation
then we expect the relation
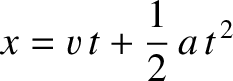 |
(3.147) |
to hold for a short time interval (i.e., in the limit
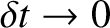 ). It follows from Equations (3.143) and (3.146)
that
). It follows from Equations (3.143) and (3.146)
that
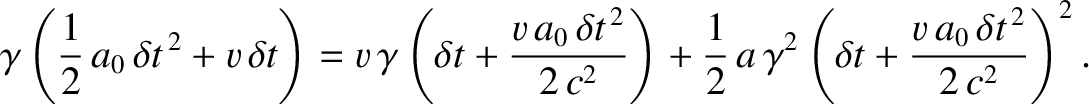 |
(3.148) |
Note that the terms in the previous equation that are first order in 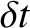 cancel one another. Equating the terms that are
second order in
cancel one another. Equating the terms that are
second order in 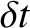 , we obtain
, we obtain
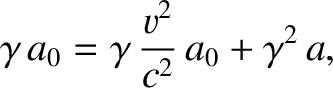 |
(3.149) |
or
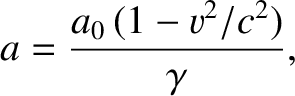 |
(3.150) |
which reduces to
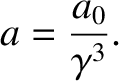 |
(3.151) |
Thus, we conclude that the particle's instantaneous acceleration in a frame of reference in which it has a finite speed is always less that that
in its instantaneous rest frame.
Given that, by definition,
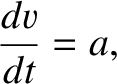 |
(3.152) |
the particle's equation of motion in  , which is assumed to be an inertial frame, is
, which is assumed to be an inertial frame, is
 |
(3.153) |
If 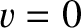 at
at  then the previous equation can be integrated to give
then the previous equation can be integrated to give
 |
(3.154) |
or
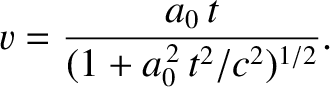 |
(3.155) |
Thus, as seen by an observer at rest in frame  , our particle initially (i.e., for
, our particle initially (i.e., for
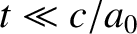 ) accelerates such that
) accelerates such that
 |
(3.156) |
in accordance with Newtonian dynamics. However, when the speed of the particle becomes comparable with the
speed of light in vacuum, the linear increase in speed with time specified in the previous equation breaks down, and, instead,
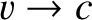 as as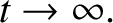 |
(3.157) |
Thus, despite the particle's constant acceleration, 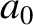 , in its instantaneous rest frame, the particle never appears to move
faster than the speed of light to a stationary observer.
, in its instantaneous rest frame, the particle never appears to move
faster than the speed of light to a stationary observer.
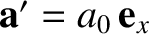 in
its instantaneous rest frame,
in
its instantaneous rest frame,  . Let the particle be located at the origin of
. Let the particle be located at the origin of  at time
at time 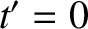 . It follows that a very short time,
. It follows that a very short time,
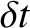 , later, the particle's spacetime coordinates in
, later, the particle's spacetime coordinates in  are
Consider a second frame of reference,
are
Consider a second frame of reference,  , that moves with velocity -
, that moves with velocity -
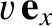 with respect to
with respect to  , and is also in a standard configuration with respect to
, and is also in a standard configuration with respect to  .
Thus, the particle's instantaneous velocity in
.
Thus, the particle's instantaneous velocity in  is
is
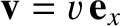 . In
. In  , the particle moves from the origin at time
, the particle moves from the origin at time  , to a point whose spacetime coordinates are
where
, to a point whose spacetime coordinates are
where
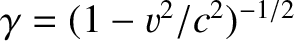 ,
a very short time later. Here, use has been made of Equations (3.104)–(3.107), as well as Equations (3.139)–(3.142). If
,
a very short time later. Here, use has been made of Equations (3.104)–(3.107), as well as Equations (3.139)–(3.142). If
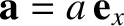 is the particle's instantaneous acceleration in
is the particle's instantaneous acceleration in
 then we expect the relation
then we expect the relation
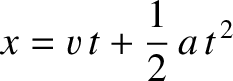
 ). It follows from Equations (3.143) and (3.146)
that
). It follows from Equations (3.143) and (3.146)
that
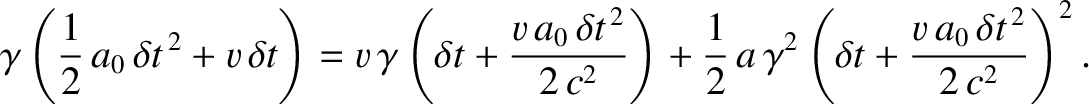
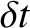 cancel one another. Equating the terms that are
second order in
cancel one another. Equating the terms that are
second order in 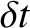 , we obtain
, we obtain
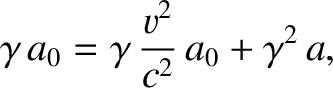
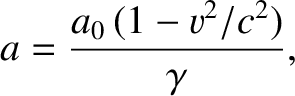
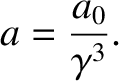
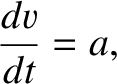
 , which is assumed to be an inertial frame, is
If
, which is assumed to be an inertial frame, is
If 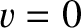 at
at  then the previous equation can be integrated to give
then the previous equation can be integrated to give

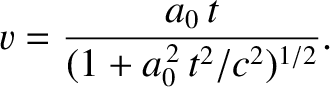
 , our particle initially (i.e., for
, our particle initially (i.e., for
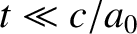 ) accelerates such that
) accelerates such that

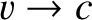 as
as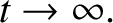
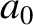 , in its instantaneous rest frame, the particle never appears to move
faster than the speed of light to a stationary observer.
, in its instantaneous rest frame, the particle never appears to move
faster than the speed of light to a stationary observer.