Next: Photons Up: Relativistic Dynamics Previous: Transformation of Energy and
Consider the situation illustrated in Figure 3.12. In the laboratory frame, a particle of rest mass 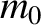 ,
moving with speed
,
moving with speed  , collides with another particle of rest mass
, collides with another particle of rest mass 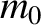 that is stationary. After the collision, the
two particles stick together, and the composite particle, whose relativistic mass is
that is stationary. After the collision, the
two particles stick together, and the composite particle, whose relativistic mass is  , moves off in the same direction as
the originally moving particle at speed
, moves off in the same direction as
the originally moving particle at speed  . Now, the relativistic mass of the originally moving particle is
. Now, the relativistic mass of the originally moving particle is
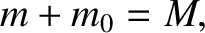 |
(3.189) |
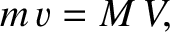 |
(3.191) |
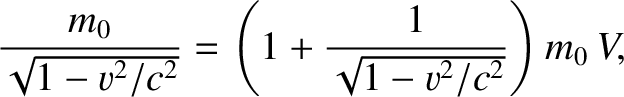 |
(3.192) |
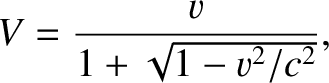 |
(3.193) |
However, there is another way of obtaining the previous equation. Let us transform to a frame of reference that moves, with respect to the laboratory frame, with
speed  parallel to the motion of the original moving particle. The composite
particle appears stationary in this reference frame. Now, if momentum is conserved, then the new reference frame is
the center-of-mass frame. (See Section 1.6.1.) Consequently, our two particles must approach one another with equal and opposite
velocities,
parallel to the motion of the original moving particle. The composite
particle appears stationary in this reference frame. Now, if momentum is conserved, then the new reference frame is
the center-of-mass frame. (See Section 1.6.1.) Consequently, our two particles must approach one another with equal and opposite
velocities,  , before the collision, as shown in the figure. However, when the transformation of velocity, (3.122), is applied to the
originally moving particle, we obtain
, before the collision, as shown in the figure. However, when the transformation of velocity, (3.122), is applied to the
originally moving particle, we obtain
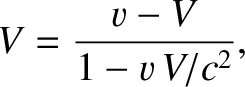 |
(3.195) |