Next: Totally Inelastic Collisions Up: Two-Particle Collisions Previous: Two-Particle Collisions
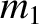 and
and 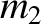 , respectively, that are free
to move in one dimension. Suppose that these two particles collide.
Suppose, further, that both particles are subject to zero net force when they are
not in contact with one another.
Finally, let us assume that we are observing the collision in a convenient inertial reference frame known as the
laboratory frame. This situation is illustrated in Figure 1.4.
, respectively, that are free
to move in one dimension. Suppose that these two particles collide.
Suppose, further, that both particles are subject to zero net force when they are
not in contact with one another.
Finally, let us assume that we are observing the collision in a convenient inertial reference frame known as the
laboratory frame. This situation is illustrated in Figure 1.4.
Both before and after the collision, the two particles move with constant velocity, in accordance with Newton's first law of motion.
Let  and
and  be the velocities of the first and second particles, respectively,
before the collision. Here, velocities to the right in Figure 1.4 are positive. Likewise, let
be the velocities of the first and second particles, respectively,
before the collision. Here, velocities to the right in Figure 1.4 are positive. Likewise, let 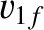 and
and 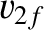 be the velocities of
the first and second particles, respectively,
after the collision. During the collision itself, the first particle exerts a large
transitory force,
be the velocities of
the first and second particles, respectively,
after the collision. During the collision itself, the first particle exerts a large
transitory force, 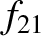 , on the second, whereas the second particle exerts an
equal and opposite force,
, on the second, whereas the second particle exerts an
equal and opposite force,
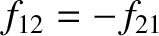 , on the first. In fact, we can model the collision
as equal and opposite impulses given to the two particles at the instant in time
when they come together. (See Section 1.3.1.)
, on the first. In fact, we can model the collision
as equal and opposite impulses given to the two particles at the instant in time
when they come together. (See Section 1.3.1.)
We are clearly considering a system in which there is zero net external force (because the forces associated with the collision are internal in nature). Hence, the total (linear) momentum of the system is a conserved quantity. (See Section 1.4.4.) Equating the total momenta before and after the collision, we obtain
This equation is valid for any one-dimensional collision, irrespective its nature.Suppose that the collision is elastic, which means that there is no associated loss of kinetic energy. Equating the net kinetic energies before and after the collision, we obtain
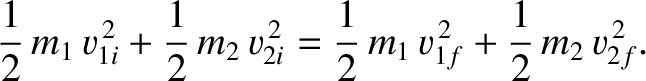 |
(1.117) |
 |
(1.118) |
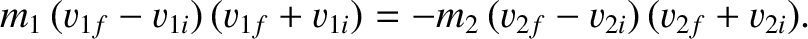 |
(1.119) |
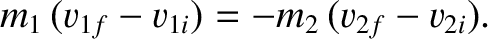 |
(1.120) |
 |
(1.121) |
Suppose that we transform to a frame of reference that co-moves with the center of mass of the system. The motion of a multi-particle system often looks particularly simple when viewed in such a frame. Because the system is subject to zero net external force, the velocity of the center of mass is invariant [see Equations (1.72)], and is given by
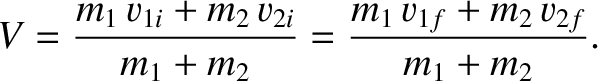 |
(1.123) |
 in the laboratory frame possesses a velocity
in the laboratory frame possesses a velocity 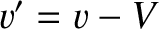 in the so-called center-of-mass
frame. It is easily demonstrated that
Note, incidentally, that the center-of-mass frame is obviously inertial (because it is moving at a constant velocity
with respect to the inertial laboratory frame).
in the so-called center-of-mass
frame. It is easily demonstrated that
Note, incidentally, that the center-of-mass frame is obviously inertial (because it is moving at a constant velocity
with respect to the inertial laboratory frame).
The previous four equations yield
where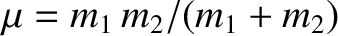 is the
so-called reduced mass (see Section 1.10.7), and
is the
so-called reduced mass (see Section 1.10.7), and
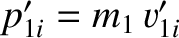 is the initial momentum of the first particle in the
center-of-mass frame, et cetera. In other words, when viewed in the center-of-mass frame, the
two particles approach one another with equal and opposite momenta before the collision,
and diverge from one another with equal and opposite momenta after the collision. See Figure 1.5.
Thus, the center-of-mass momentum conservation equation,
is the initial momentum of the first particle in the
center-of-mass frame, et cetera. In other words, when viewed in the center-of-mass frame, the
two particles approach one another with equal and opposite momenta before the collision,
and diverge from one another with equal and opposite momenta after the collision. See Figure 1.5.
Thus, the center-of-mass momentum conservation equation,
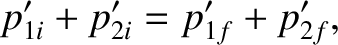 |
(1.130) |
Equations (1.122), (1.128), and (1.129) can be combined to give
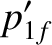 |
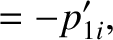 |
(1.131) |
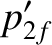 |
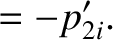 |
(1.132) |
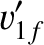 |
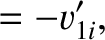 |
(1.133) |
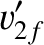 |
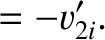 |
(1.134) |
Equations (1.124) and (1.125) can be combined with the previous two equations to give
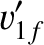 |
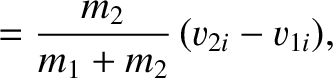 |
(1.135) |
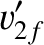 |
 |
(1.136) |
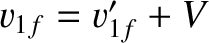 and
and
 , which allows us to express the
velocities of the two particles after the collision in the laboratory frame in terms of the corresponding velocities before the collision:
, which allows us to express the
velocities of the two particles after the collision in the laboratory frame in terms of the corresponding velocities before the collision:
Let us, now, consider some special cases. Suppose that two equal-mass particles collide elastically.
If  then Equations (1.137) and (1.138) yield
then Equations (1.137) and (1.138) yield
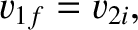 |
(1.139) |
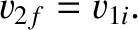 |
(1.140) |
 then the first particle is brought to a halt whereas the second particle
moves off with velocity
then the first particle is brought to a halt whereas the second particle
moves off with velocity  . It is possible to reproduce this effect in snooker or pool
by striking the cue ball with great force in such a manner that it slides, rather
that rolls, over the table; in this case, when the cue ball strikes another ball head-on
it comes to a complete halt, and the other ball is propelled forward very rapidly.
Incidentally, it is necessary to prevent the cue ball from rolling, because rolling motion
is not taken into account in our analysis, and actually changes the answer.
. It is possible to reproduce this effect in snooker or pool
by striking the cue ball with great force in such a manner that it slides, rather
that rolls, over the table; in this case, when the cue ball strikes another ball head-on
it comes to a complete halt, and the other ball is propelled forward very rapidly.
Incidentally, it is necessary to prevent the cue ball from rolling, because rolling motion
is not taken into account in our analysis, and actually changes the answer.
Suppose that the second particle is much more massive than the first (i.e.,
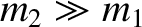 ),
and is initially at rest (i.e.,
),
and is initially at rest (i.e., 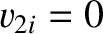 ). In this case, Equations (1.137) and (1.138) yield
). In this case, Equations (1.137) and (1.138) yield
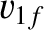 |
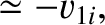 |
(1.141) |
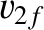 |
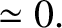 |
(1.142) |
Suppose, finally, that the second particle is much lighter than the first (i.e.,
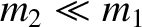 ),
and is initially at rest (i.e.,
),
and is initially at rest (i.e., 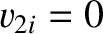 ). In this case, Equations (1.137) and (1.138) yield
). In this case, Equations (1.137) and (1.138) yield
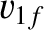 |
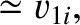 |
(1.143) |
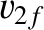 |
 |
(1.144) |