In a totally inelastic
collision, the two particles stick together after colliding, so that they
end up moving with the same final velocity,
 . In this case,
. In this case,
 |
(1.145) |
In other words, the common final velocity of the two particles is equal to the
center-of-mass velocity of the system. This is hardly a surprising result. We have already seen
that in the center-of-mass frame the two particles must diverge with equal and opposite momenta after
the collision. However, in a totally inelastic collision these two momenta must
also be equal (because the two objects stick together). The only way in which this is possible
is if the two particles remain stationary in the center-of-mass frame after the collision.
Hence, after the collision, the two particles move with the center-of-mass velocity in the laboratory frame.
Suppose that the second object is initially at rest (i.e., 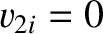 ) in the laboratory frame. In this
special case, the common final velocity of the two objects is
) in the laboratory frame. In this
special case, the common final velocity of the two objects is
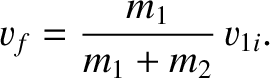 |
(1.146) |
Note that the first object is slowed down by the collision.
The fractional loss in kinetic energy of the system due to the collision is given
by
 |
(1.147) |
The loss in kinetic energy is small if the (initially) stationary object
is much lighter than the moving object (i.e., if
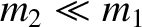 ), and almost
), and almost 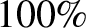 if the moving
object is much lighter than the stationary one (i.e., if
if the moving
object is much lighter than the stationary one (i.e., if
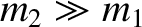 ).
Of course, the lost kinetic energy of the
system is converted into some other form of energy; for instance, heat energy.
).
Of course, the lost kinetic energy of the
system is converted into some other form of energy; for instance, heat energy.
 . In this case,
. In this case,

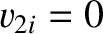 ) in the laboratory frame. In this
special case, the common final velocity of the two objects is
) in the laboratory frame. In this
special case, the common final velocity of the two objects is
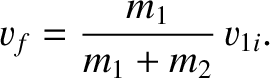

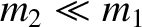 ), and almost
), and almost 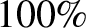 if the moving
object is much lighter than the stationary one (i.e., if
if the moving
object is much lighter than the stationary one (i.e., if
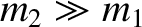 ).
Of course, the lost kinetic energy of the
system is converted into some other form of energy; for instance, heat energy.
).
Of course, the lost kinetic energy of the
system is converted into some other form of energy; for instance, heat energy.