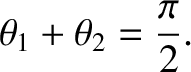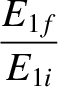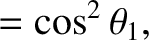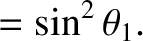Suppose that an object of mass 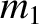 , moving with initial velocity
, moving with initial velocity
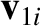 , strikes a
second object, of mass
, strikes a
second object, of mass 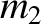 , that is initially at rest. Suppose, further, that the collision
is not head-on, so that after the collision the first object moves off at an angle
, that is initially at rest. Suppose, further, that the collision
is not head-on, so that after the collision the first object moves off at an angle 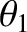 to
its initial direction of motion, whereas the second object recoils at an angle
to
its initial direction of motion, whereas the second object recoils at an angle 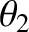 to
this direction. Let the final velocities of the two objects be
to
this direction. Let the final velocities of the two objects be
 and
and
 , respectively. See Figure 1.6.
, respectively. See Figure 1.6.
Figure 1.6:
A two-dimensional collision in the laboratory frame.
|
|
We are again considering a system in which there is zero net external force (because the forces associated
with the collision are internal in nature). It follows that the total momentum of
the system is a conserved quantity. However, unlike before, we must now treat
momentum as a vector quantity, because we are no longer dealing with one-dimensional
motion. Momentum conservation implies that
 |
(1.148) |
As before, it is convenient to transform to a frame of reference that co-moves with the center of mass
of the system. The invariant velocity of the center of mass is given by
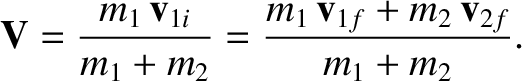 |
(1.149) |
An object that possesses a velocity  in the laboratory frame possesses a velocity
in the laboratory frame possesses a velocity
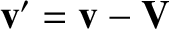 in the center-of-mass frame. Hence, it follows that
in the center-of-mass frame. Hence, it follows that
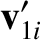 |
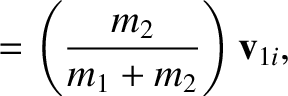 |
(1.150) |
 |
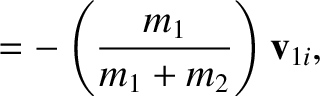 |
(1.151) |
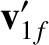 |
 |
(1.152) |
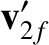 |
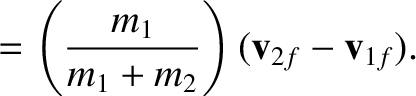 |
(1.153) |
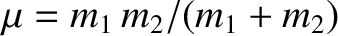 . (Of course,
. (Of course,
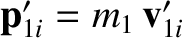 , et cetera.)
As before, in the center-of-mass frame, the two objects approach
one another with equal and opposite momenta before the collision, and diverge from
one another with equal and opposite momenta after the collision. Let
, et cetera.)
As before, in the center-of-mass frame, the two objects approach
one another with equal and opposite momenta before the collision, and diverge from
one another with equal and opposite momenta after the collision. Let
 be the direction subtended between the final and initial
momenta of each object in the center-of-mass frame. See Figure 1.7.
It follows that in the
be the direction subtended between the final and initial
momenta of each object in the center-of-mass frame. See Figure 1.7.
It follows that in the  -
- coordinate system shown in the figure,
where
coordinate system shown in the figure,
where
 , et cetera.
Finally, if the collision is elastic then the kinetic energy before the collision must equal that after the
collision (in both the laboratory and the center-of-mass frames). It follows that
, et cetera.
Finally, if the collision is elastic then the kinetic energy before the collision must equal that after the
collision (in both the laboratory and the center-of-mass frames). It follows that
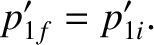 |
(1.160) |
Hence,
It can be seen from the previous two equations that an elastic two-dimensional collision is fully
characterized once the initial velocity,  , and the scattering angle,
, and the scattering angle,  , are specified.
In general, we would expect
, are specified.
In general, we would expect  to be able to take all values in the range 0 to
to be able to take all values in the range 0 to 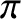 .
In fact, a head-on collision corresponds to
.
In fact, a head-on collision corresponds to
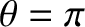 , whereas a glancing collision corresponds to
, whereas a glancing collision corresponds to
 .
.
Figure 1.7:
A two-dimensional collision in the center-of-mass frame.
|
|
Now,
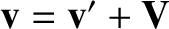 ,
where
,
where
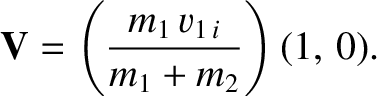 |
(1.163) |
It follows that, in the  -
- coordinate system shown in Figure 1.6, the laboratory-frame velocities of the two objects after the collision are
Hence, according to Figure 1.6,
The last equation implies that
coordinate system shown in Figure 1.6, the laboratory-frame velocities of the two objects after the collision are
Hence, according to Figure 1.6,
The last equation implies that
 |
(1.168) |
Differentiating Equation (1.166) with respect to  , we obtain
, we obtain
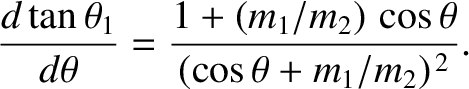 |
(1.169) |
Thus,
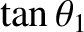 attains an extreme value, which can be shown to correspond to a maximum
possible value of
attains an extreme value, which can be shown to correspond to a maximum
possible value of 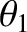 , when the numerator of the previous expression is zero;
that is, when
, when the numerator of the previous expression is zero;
that is, when
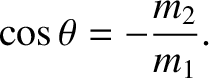 |
(1.170) |
Note that it is only possible to solve the previous equation when 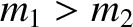 .
If this is the case then Equation (1.166) yields
.
If this is the case then Equation (1.166) yields
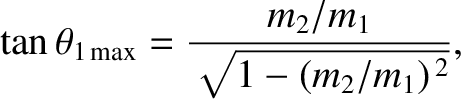 |
(1.171) |
which reduces to
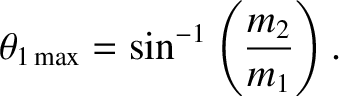 |
(1.172) |
Hence, we conclude that when 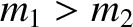 there is a maximum possible
value of the scattering angle,
there is a maximum possible
value of the scattering angle, 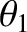 , in the laboratory frame. This maximum
value is always less than
, in the laboratory frame. This maximum
value is always less than 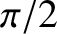 , which implies that there is
no backward scattering (i.e.,
, which implies that there is
no backward scattering (i.e.,
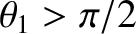 ) at all when
) at all when 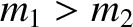 . For the special case when
. For the special case when
 , the maximum scattering angle is
, the maximum scattering angle is 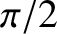 . However, for
. However, for
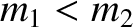 there is no maximum value, and the scattering angle in the laboratory frame can thus
range all the way to
there is no maximum value, and the scattering angle in the laboratory frame can thus
range all the way to 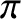 .
.
Suppose that the two particles have equal masses, so that  . In this case, Equation (1.166)
yields
. In this case, Equation (1.166)
yields
 |
(1.173) |
Hence,
 |
(1.174) |
In other words, the scattering angle of the first particle in the laboratory
frame is half of the scattering angle in the center-of-mass frame.
The previous equation can be combined with Equation (1.168) to
give
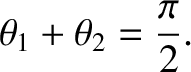 |
(1.175) |
Thus, in the laboratory frame, the two particles move off at right-angles to one another after the collision.
It is possible to reproduce this effect in snooker or pool
by striking the cue ball with great force in such a manner that it slides, rather
that rolls, over the table; in this case, when the cue ball strikes another ball obliquely
then the two balls move off at right-angles to one another.
Incidentally, it is necessary to prevent the cue ball from rolling, because rolling motion
is not taken into account in our analysis, and actually changes the answer.
Finally, it is easily demonstrated that the fractions of the initial kinetic energy carried off by the
two particles after the collision are
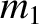 , moving with initial velocity
, moving with initial velocity
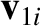 , strikes a
second object, of mass
, strikes a
second object, of mass 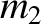 , that is initially at rest. Suppose, further, that the collision
is not head-on, so that after the collision the first object moves off at an angle
, that is initially at rest. Suppose, further, that the collision
is not head-on, so that after the collision the first object moves off at an angle 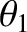 to
its initial direction of motion, whereas the second object recoils at an angle
to
its initial direction of motion, whereas the second object recoils at an angle 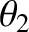 to
this direction. Let the final velocities of the two objects be
to
this direction. Let the final velocities of the two objects be
 and
and
 , respectively. See Figure 1.6.
, respectively. See Figure 1.6.

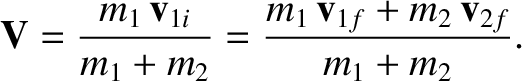
 in the laboratory frame possesses a velocity
in the laboratory frame possesses a velocity
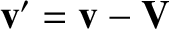 in the center-of-mass frame. Hence, it follows that
in the center-of-mass frame. Hence, it follows that
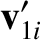
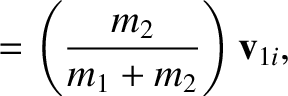

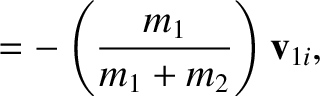
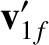

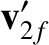
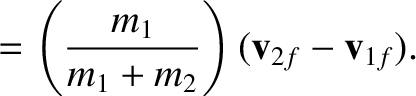
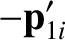
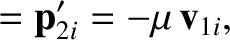
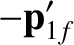
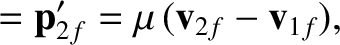
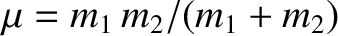 . (Of course,
. (Of course,
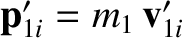 , et cetera.)
As before, in the center-of-mass frame, the two objects approach
one another with equal and opposite momenta before the collision, and diverge from
one another with equal and opposite momenta after the collision. Let
, et cetera.)
As before, in the center-of-mass frame, the two objects approach
one another with equal and opposite momenta before the collision, and diverge from
one another with equal and opposite momenta after the collision. Let
 be the direction subtended between the final and initial
momenta of each object in the center-of-mass frame. See Figure 1.7.
It follows that in the
be the direction subtended between the final and initial
momenta of each object in the center-of-mass frame. See Figure 1.7.
It follows that in the  -
- coordinate system shown in the figure,
where
coordinate system shown in the figure,
where
 , et cetera.
Finally, if the collision is elastic then the kinetic energy before the collision must equal that after the
collision (in both the laboratory and the center-of-mass frames). It follows that
, et cetera.
Finally, if the collision is elastic then the kinetic energy before the collision must equal that after the
collision (in both the laboratory and the center-of-mass frames). It follows that
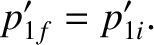
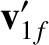
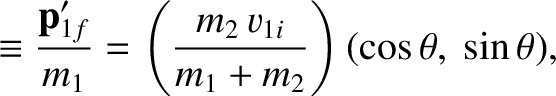
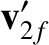
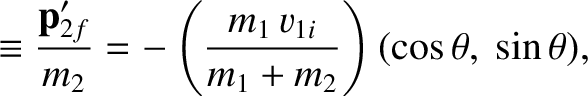
 , and the scattering angle,
, and the scattering angle,  , are specified.
In general, we would expect
, are specified.
In general, we would expect  to be able to take all values in the range 0 to
to be able to take all values in the range 0 to 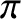 .
In fact, a head-on collision corresponds to
.
In fact, a head-on collision corresponds to
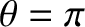 , whereas a glancing collision corresponds to
, whereas a glancing collision corresponds to
 .
.
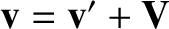 ,
where
,
where
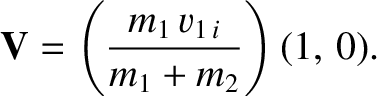
 -
- coordinate system shown in Figure 1.6, the laboratory-frame velocities of the two objects after the collision are
Hence, according to Figure 1.6,
coordinate system shown in Figure 1.6, the laboratory-frame velocities of the two objects after the collision are
Hence, according to Figure 1.6,

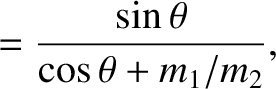
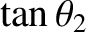
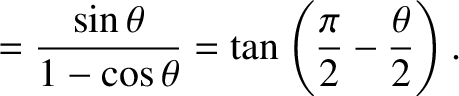
 , we obtain
, we obtain
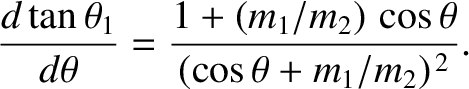
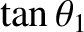 attains an extreme value, which can be shown to correspond to a maximum
possible value of
attains an extreme value, which can be shown to correspond to a maximum
possible value of 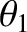 , when the numerator of the previous expression is zero;
that is, when
, when the numerator of the previous expression is zero;
that is, when
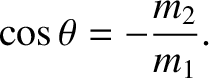
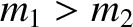 .
If this is the case then Equation (1.166) yields
.
If this is the case then Equation (1.166) yields
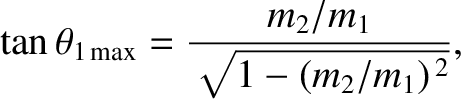
 there is a maximum possible
value of the scattering angle,
there is a maximum possible
value of the scattering angle, 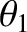 , in the laboratory frame. This maximum
value is always less than
, in the laboratory frame. This maximum
value is always less than 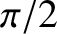 , which implies that there is
no backward scattering (i.e.,
, which implies that there is
no backward scattering (i.e.,
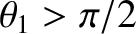 ) at all when
) at all when 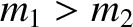 . For the special case when
. For the special case when
 , the maximum scattering angle is
, the maximum scattering angle is 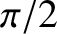 . However, for
. However, for
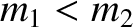 there is no maximum value, and the scattering angle in the laboratory frame can thus
range all the way to
there is no maximum value, and the scattering angle in the laboratory frame can thus
range all the way to 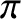 .
.
 . In this case, Equation (1.166)
yields
. In this case, Equation (1.166)
yields