Relativistic Energy-Momentum Relation
According to Equations (3.162), (3.165), and (3.174), a particle of rest mass 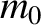 , moving at velocity
, moving at velocity
 , has a relativistic momentum
, has a relativistic momentum
 |
(3.176) |
and a relativistic energy
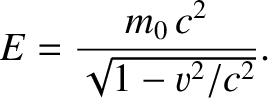 |
(3.177) |
Thus,
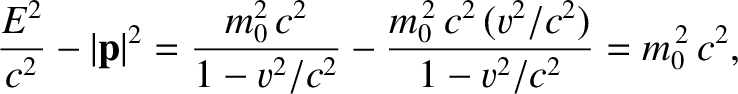 |
(3.178) |
which leads to the relativistic energy-momentum relation,
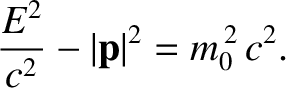 |
(3.179) |
Now, given that the rest mass is independent of the particle's motion (i.e., it is the same in all inertial frames of reference), we
deduce that
 takes the same value in all inertial frames of reference.
takes the same value in all inertial frames of reference.
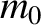 , moving at velocity
, moving at velocity
 , has a relativistic momentum
, has a relativistic momentum

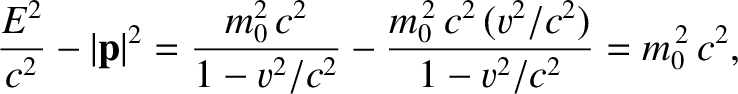
 takes the same value in all inertial frames of reference.
takes the same value in all inertial frames of reference.