Next: Compton Scattering Up: Relativistic Dynamics Previous: Relativistic Doppler Effect
Consider the situation illustrated in Figure 3.13. A radiation source that is located at the origin of reference frame  emits electromagnetic radiation of angular frequency
emits electromagnetic radiation of angular frequency  , whose direction of propagation lies in the
, whose direction of propagation lies in the  -
- plane
and subtends an angle
plane
and subtends an angle  with the
with the  -axis. It follows that the wavevector of the radiation has the
non-zero components
-axis. It follows that the wavevector of the radiation has the
non-zero components
 |
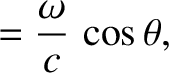 |
(3.214) |
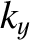 |
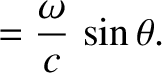 |
(3.215) |
 that moves with velocity
that moves with velocity
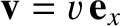 , and is in a standard configuration, with respect to
, and is in a standard configuration, with respect to  .
In
.
In  , let
, let 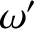 be the angular frequency of the radiation, and let
be the angular frequency of the radiation, and let  be the angle subtended by its direction
of propagation and the
be the angle subtended by its direction
of propagation and the 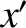 -axis. It follows that, in
-axis. It follows that, in  , the wavevector of the radiation has the
non-zero components
, the wavevector of the radiation has the
non-zero components
 |
 |
(3.216) |
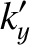 |
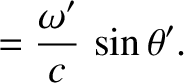 |
(3.217) |
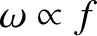 , we deduce that
, we deduce that
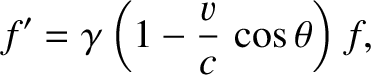 |
(3.221) |
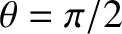 , so that the radiation is propagating in a direction that is perpendicular
to the relative velocity of the source and the observer, then
, so that the radiation is propagating in a direction that is perpendicular
to the relative velocity of the source and the observer, then
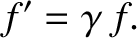 |
(3.222) |
Finally, Equations (3.218) and (3.219) can be combined to give
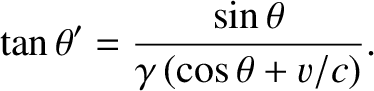 |
(3.223) |