Compton Scattering
Figure 3.14:
Compton Scattering.
|
|
Compton scattering occurs when X-rays scatter off electrons in ordinary matter. The result is an increase in the
wavelength of the scattered X-rays. This increase is inexplicable within the context of classical physics, which
predicts that radiation that scatters off a stationary target should suffer no change in wavelength. In fact, as we shall explain, this
effect can be explained in terms of the scattering of individual X-ray photons by individual electrons.
Consider the situation, illustrated in Figure 3.14, in which an X-ray photon of momentum
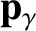 collides with
a stationary electron of rest mass
collides with
a stationary electron of rest mass 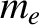 . After the collision, the momentum of the photon is
. After the collision, the momentum of the photon is
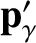 ,
and the recoil momentum of the electron is
,
and the recoil momentum of the electron is
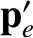 . Conservation of momentum in the collision requires that
. Conservation of momentum in the collision requires that
 |
(3.224) |
However, we know that
where  and
and  are the photon's initial and final wavevector, respectively,
are the photon's initial and final wavevector, respectively,  is the electron's
recoil speed, and
is the electron's
recoil speed, and
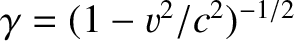 . [See Equations (3.162) and (3.200).] Thus, we obtain
. [See Equations (3.162) and (3.200).] Thus, we obtain
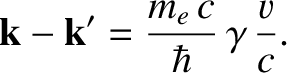 |
(3.228) |
The previous equation yields
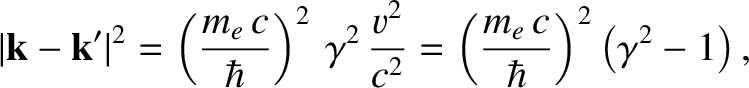 |
(3.229) |
or
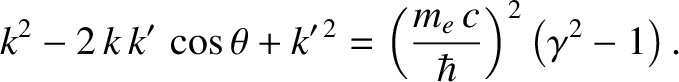 |
(3.230) |
Here,  is the angle through which the photon is scattered (i.e., the angle subtended between
is the angle through which the photon is scattered (i.e., the angle subtended between  and
and  ). See Figure 3.14.
). See Figure 3.14.
Let 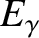 ,
, 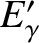 ,
, 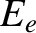 , and
, and  be the initial photon energy, the final photon energy, the
initial electron energy, and the final electron energy, respectively. Energy conservation in the collision requires that
be the initial photon energy, the final photon energy, the
initial electron energy, and the final electron energy, respectively. Energy conservation in the collision requires that
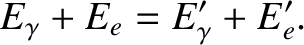 |
(3.231) |
However, we know that
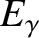 |
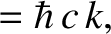 |
(3.232) |
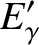 |
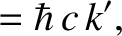 |
(3.233) |
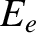 |
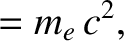 |
(3.234) |
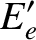 |
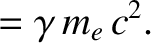 |
(3.235) |
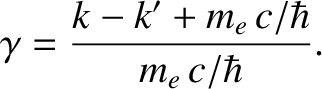 |
(3.236) |
Equations (3.230) and (3.236) can be combined to give
 |
(3.237) |
or
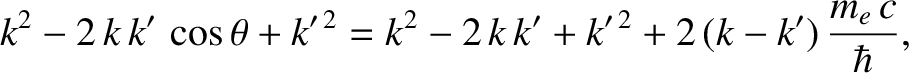 |
(3.238) |
which can be rearranged to produce
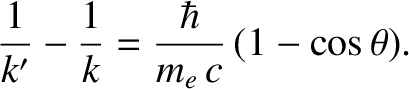 |
(3.239) |
Finally, if
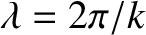 and
and
 are the initial and final wavelengths of the photon then we
obtain
are the initial and final wavelengths of the photon then we
obtain
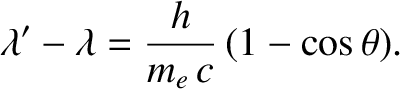 |
(3.240) |
The previous equation relates the increase in wavelength of the scattered photon to its scattering angle in a simple
manner. Here,
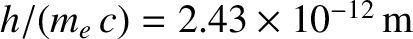 is known as the Compton wavelength of the electron. The
previous formula was verified experimentally by Arthur Compton in 1923.
is known as the Compton wavelength of the electron. The
previous formula was verified experimentally by Arthur Compton in 1923.
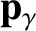 collides with
a stationary electron of rest mass
collides with
a stationary electron of rest mass 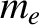 . After the collision, the momentum of the photon is
. After the collision, the momentum of the photon is
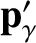 ,
and the recoil momentum of the electron is
,
and the recoil momentum of the electron is
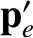 . Conservation of momentum in the collision requires that
. Conservation of momentum in the collision requires that


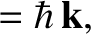
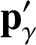
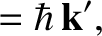
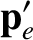

 and
and  are the photon's initial and final wavevector, respectively,
are the photon's initial and final wavevector, respectively,  is the electron's
recoil speed, and
is the electron's
recoil speed, and
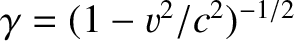 . [See Equations (3.162) and (3.200).] Thus, we obtain
. [See Equations (3.162) and (3.200).] Thus, we obtain
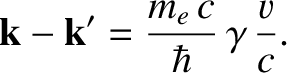
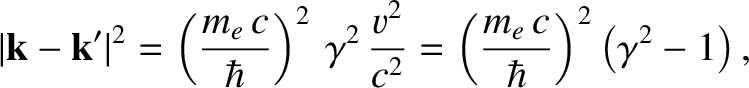
 is the angle through which the photon is scattered (i.e., the angle subtended between
is the angle through which the photon is scattered (i.e., the angle subtended between  and
and  ). See Figure 3.14.
). See Figure 3.14.
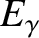 ,
, 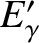 ,
, 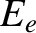 , and
, and  be the initial photon energy, the final photon energy, the
initial electron energy, and the final electron energy, respectively. Energy conservation in the collision requires that
be the initial photon energy, the final photon energy, the
initial electron energy, and the final electron energy, respectively. Energy conservation in the collision requires that
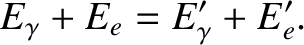
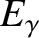
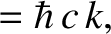
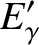
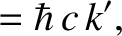
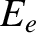
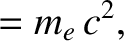
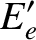
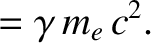

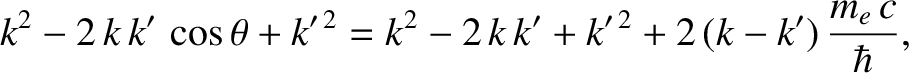
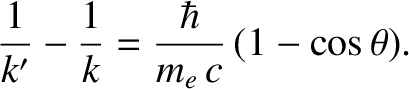
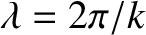 and
and
 are the initial and final wavelengths of the photon then we
obtain
are the initial and final wavelengths of the photon then we
obtain
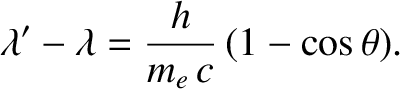
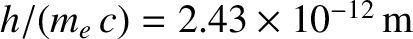 is known as the Compton wavelength of the electron. The
previous formula was verified experimentally by Arthur Compton in 1923.
is known as the Compton wavelength of the electron. The
previous formula was verified experimentally by Arthur Compton in 1923.