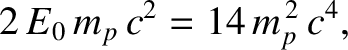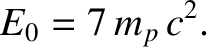Figure 3.15:
Pair creation.
|
|
Finally, consider the situation, illustrated in Figure 3.15, in which a moving proton collides with a
stationary proton, and a proton/anti-proton pair is created during the collision. We wish to determine the
minimum energy of the incident proton required to create the pair. Let 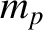 be the proton rest mass.
As is clear from the figure, in the center of mass frame, the minimum energy state corresponds to the case in
which the particles are all at rest after the collision. (Additional energy would just causes the particles to move away from one another, in this frame, after the collision.) Thus, in the laboratory frame, the particles must all move
with a common velocity after the collision. However, given that the particles all have the same mass, each
particle in the laboratory frame must have momentum
be the proton rest mass.
As is clear from the figure, in the center of mass frame, the minimum energy state corresponds to the case in
which the particles are all at rest after the collision. (Additional energy would just causes the particles to move away from one another, in this frame, after the collision.) Thus, in the laboratory frame, the particles must all move
with a common velocity after the collision. However, given that the particles all have the same mass, each
particle in the laboratory frame must have momentum 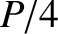 , after the collision, where
, after the collision, where  is the total momentum of the
system, and must have energy
is the total momentum of the
system, and must have energy  , where
, where  is the total energy of the system. Thus, the energy-momentum relation [see Equation (3.179)] for one of the particles after the collision yields
is the total energy of the system. Thus, the energy-momentum relation [see Equation (3.179)] for one of the particles after the collision yields
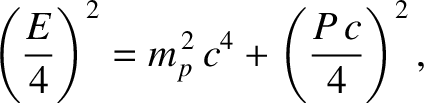 |
(3.241) |
or
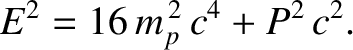 |
(3.242) |
Let 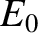 be the initial laboratory-frame energy of the moving proton before the collision. Energy
conservation requires that
be the initial laboratory-frame energy of the moving proton before the collision. Energy
conservation requires that
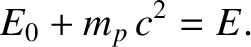 |
(3.243) |
The previous two equations can be combined to give
 |
(3.244) |
or
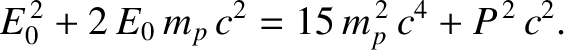 |
(3.245) |
However, the initial momentum of the moving proton in the laboratory frame is  (because the proton possesses all of the system's initial momentum, and the total momentum must be the same before and after the collision). Hence, the moving proton's initial energy-momentum
relation [see Equation (3.179)] is
(because the proton possesses all of the system's initial momentum, and the total momentum must be the same before and after the collision). Hence, the moving proton's initial energy-momentum
relation [see Equation (3.179)] is
 |
(3.246) |
The previous two equations yield
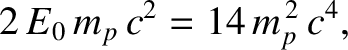 |
(3.247) |
or
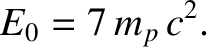 |
(3.248) |
Thus, the minimum kinetic energy of the incident proton required to generate a proton/anti-proton pair is
6 times its rest mass energy. This corresponds to a Lorentz factor of 7, which implies a speed of about 99% of the speed of
light in vacuum.
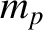 be the proton rest mass.
As is clear from the figure, in the center of mass frame, the minimum energy state corresponds to the case in
which the particles are all at rest after the collision. (Additional energy would just causes the particles to move away from one another, in this frame, after the collision.) Thus, in the laboratory frame, the particles must all move
with a common velocity after the collision. However, given that the particles all have the same mass, each
particle in the laboratory frame must have momentum
be the proton rest mass.
As is clear from the figure, in the center of mass frame, the minimum energy state corresponds to the case in
which the particles are all at rest after the collision. (Additional energy would just causes the particles to move away from one another, in this frame, after the collision.) Thus, in the laboratory frame, the particles must all move
with a common velocity after the collision. However, given that the particles all have the same mass, each
particle in the laboratory frame must have momentum 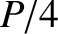 , after the collision, where
, after the collision, where  is the total momentum of the
system, and must have energy
is the total momentum of the
system, and must have energy  , where
, where  is the total energy of the system. Thus, the energy-momentum relation [see Equation (3.179)] for one of the particles after the collision yields
is the total energy of the system. Thus, the energy-momentum relation [see Equation (3.179)] for one of the particles after the collision yields
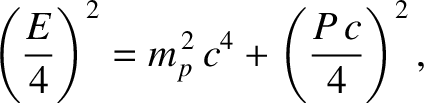
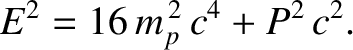
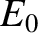 be the initial laboratory-frame energy of the moving proton before the collision. Energy
conservation requires that
be the initial laboratory-frame energy of the moving proton before the collision. Energy
conservation requires that
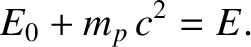

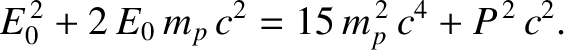
 (because the proton possesses all of the system's initial momentum, and the total momentum must be the same before and after the collision). Hence, the moving proton's initial energy-momentum
relation [see Equation (3.179)] is
(because the proton possesses all of the system's initial momentum, and the total momentum must be the same before and after the collision). Hence, the moving proton's initial energy-momentum
relation [see Equation (3.179)] is