Next: Effect of Electromagnetic Torques Up: Toroidal Tearing Modes Previous: Linear Calculation Contents
 tearing mode that reconnects magnetic flux principally at the
tearing mode that reconnects magnetic flux principally at the  th rational surface in our example tokamak plasma. Let us now suppose that the amount of reconnected magnetic
flux is sufficiently large that the plasma response at this surface lies in the nonlinear regime, which is equivalent to supposing that the
magnetic island width at the
th rational surface in our example tokamak plasma. Let us now suppose that the amount of reconnected magnetic
flux is sufficiently large that the plasma response at this surface lies in the nonlinear regime, which is equivalent to supposing that the
magnetic island width at the  th rational surface is much greater than the linear layer width. (See Section 5.16.)
Given that the mode is assumed not to interact
strongly with the other rational surfaces in the plasma, due to the assumed strong shielding present at these surfaces, the analysis of Chapter 12
implies that the frequency of the mode can be written [10,18]
th rational surface is much greater than the linear layer width. (See Section 5.16.)
Given that the mode is assumed not to interact
strongly with the other rational surfaces in the plasma, due to the assumed strong shielding present at these surfaces, the analysis of Chapter 12
implies that the frequency of the mode can be written [10,18]
 |
(14.150) |
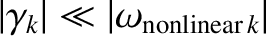 , and
Here, the impurity ion diamagnetic frequency profile,
, and
Here, the impurity ion diamagnetic frequency profile,
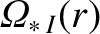 , is defined in Equation (A.78). Moreover, the
dimensionless neoclassical quantities,
, is defined in Equation (A.78). Moreover, the
dimensionless neoclassical quantities,
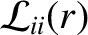 and
and
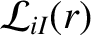 , are defined in Equation (A.80).
The previous two equations are a generalization of Equation (12.11) that takes the presence of impurity ions in the plasma
into account, does not assume a small fraction of trapped particles, and does not assume that the plasma at the
, are defined in Equation (A.80).
The previous two equations are a generalization of Equation (12.11) that takes the presence of impurity ions in the plasma
into account, does not assume a small fraction of trapped particles, and does not assume that the plasma at the  th rational surface is in the banana collisionality regime [11,14,16]. The previous two equations imply that a nonlinear tearing mode is entrained by the ion fluid at the
th rational surface is in the banana collisionality regime [11,14,16]. The previous two equations imply that a nonlinear tearing mode is entrained by the ion fluid at the  th rational surface.
It follows from
Equation (14.130) that the normalized mode rotation frequency at the
th rational surface.
It follows from
Equation (14.130) that the normalized mode rotation frequency at the 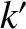 th rational surface, where
th rational surface, where  , is
where the nonlinear natural frequencies,
, is
where the nonlinear natural frequencies,
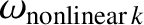 , are specified in Table 14.5. Here, we have again neglected the comparatively small growth-rate of the mode with respect to its comparatively large real frequency in the laboratory frame. Note that the nonlinear natural frequencies are all
significantly different from one another, and are also significantly different from the linear natural frequencies.
, are specified in Table 14.5. Here, we have again neglected the comparatively small growth-rate of the mode with respect to its comparatively large real frequency in the laboratory frame. Note that the nonlinear natural frequencies are all
significantly different from one another, and are also significantly different from the linear natural frequencies.
If we repeat the calculation made in the previous section, replacing the  values specified in Equation (14.143) with those specified
in Equation (14.152), then we obtain the results shown in Table 14.7. As before, it can be seen that
values specified in Equation (14.143) with those specified
in Equation (14.152), then we obtain the results shown in Table 14.7. As before, it can be seen that
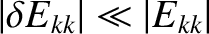 for all possible nonlinear
for all possible nonlinear  tearing modes. Thus, the fact that nonlinear tearing modes effectively corotate with the ion fluid, rather than the electron fluid, does not change the
conclusion of the previous section that there is sufficient rotational shear present in the plasma to ensure that a nonlinear
tearing modes. Thus, the fact that nonlinear tearing modes effectively corotate with the ion fluid, rather than the electron fluid, does not change the
conclusion of the previous section that there is sufficient rotational shear present in the plasma to ensure that a nonlinear  tearing mode can only reconnect magnetic flux at one rational surface at a time.
tearing mode can only reconnect magnetic flux at one rational surface at a time.
Thus, we have effectively answered the question posed at the end of Section 14.13. The full shielding response model most accurately describes a tearing mode in a realistic tokamak plasma. Note that plasmas in tokamak fusion reactor reactors are likely to possess significantly less rotation shear than KSTAR plasmas (because they will not rotate as fast as KSTAR plasmas—see Section 5.15), but much larger Lundquist numbers. The two effects largely offset one another. Hence, we conclude that the full shielding response model is also likely to apply to tokamak fusion reactors.