Next: Nonlinear Calculation Up: Toroidal Tearing Modes Previous: Example Tokamak Discharge Contents
 tearing mode that reconnects magnetic flux principally at the
tearing mode that reconnects magnetic flux principally at the  th rational surface in our example tokamak plasma. Let us suppose that the amount of reconnected magnetic
flux is sufficiently small that the plasma response at this surface lies in the linear regime, which is equivalent to supposing that the
magnetic island width at the
th rational surface in our example tokamak plasma. Let us suppose that the amount of reconnected magnetic
flux is sufficiently small that the plasma response at this surface lies in the linear regime, which is equivalent to supposing that the
magnetic island width at the  th rational surface is much less than the linear layer width. (See Section 5.16.)
Given that the mode is assumed not to interact
strongly with the other rational surfaces in the plasma, due to the assumed strong shielding present at these surfaces, the analysis of Chapter 6
implies that the frequency of the mode can be written
th rational surface is much less than the linear layer width. (See Section 5.16.)
Given that the mode is assumed not to interact
strongly with the other rational surfaces in the plasma, due to the assumed strong shielding present at these surfaces, the analysis of Chapter 6
implies that the frequency of the mode can be written
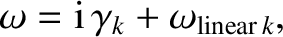 |
(14.141) |
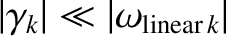 , and
, and
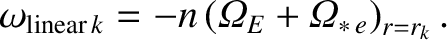 |
(14.142) |
 th rational surface. It follows from
Equation (14.130) that the normalized mode rotation frequency at the
th rational surface. It follows from
Equation (14.130) that the normalized mode rotation frequency at the 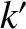 th rational surface, where
th rational surface, where  , is
Here, we have neglected the comparatively small growth-rate of the mode with respect to its comparatively large real frequency in the laboratory frame.
, is
Here, we have neglected the comparatively small growth-rate of the mode with respect to its comparatively large real frequency in the laboratory frame.
According to Equations (14.120) and (14.123), the linear dispersion relation of our tearing mode can be written
with for ,
where
,
where
Table 14.4 shows the dimensionless layer matching parameters,
 ,
where
,
where  , calculated from the layer parameters given in Table 14.3, with the
, calculated from the layer parameters given in Table 14.3, with the
 specified by Equation (14.143). It can be seen that all of the
specified by Equation (14.143). It can be seen that all of the
 have magnitudes that are much greater
than unity, indicating a strong shielding response at the rational surfaces other than the
have magnitudes that are much greater
than unity, indicating a strong shielding response at the rational surfaces other than the  th surface. This strong shielding is a consequence of
sheared rotation in the plasma [14]. Roughly speaking, a given rational surface can only reconnect magnetic flux that corotates with the
local electron fluid. However, as a consequence of sheared rotation, if a tearing perturbation corotates with the local electron fluid at
a given rational surface in the plasma then it does not corotate with the local electron fluids at any of the other surfaces. This is
illustrated in Table 14.5, which specifies the linear natural frequencies,
th surface. This strong shielding is a consequence of
sheared rotation in the plasma [14]. Roughly speaking, a given rational surface can only reconnect magnetic flux that corotates with the
local electron fluid. However, as a consequence of sheared rotation, if a tearing perturbation corotates with the local electron fluid at
a given rational surface in the plasma then it does not corotate with the local electron fluids at any of the other surfaces. This is
illustrated in Table 14.5, which specifies the linear natural frequencies,
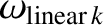 , associated with the various
, associated with the various  rational
surfaces present in the plasma. It is clear that the natural frequencies all differ substantially from one another. Consequently, a linear
rational
surfaces present in the plasma. It is clear that the natural frequencies all differ substantially from one another. Consequently, a linear  tearing mode
can only reconnect
magnetic flux at one rational surface at a time in the plasma.
tearing mode
can only reconnect
magnetic flux at one rational surface at a time in the plasma.
Treating
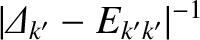 as a small parameter, Equation (14.145), yields
as a small parameter, Equation (14.145), yields
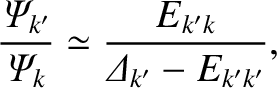 |
(14.147) |
 ,
which implies that
,
which implies that
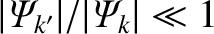 . In other words, the strong rotational shielding present at the
. In other words, the strong rotational shielding present at the 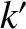 th rational surface does indeed ensure that
very little magnetic flux is reconnected at that surface compared to that reconnected at the
th rational surface does indeed ensure that
very little magnetic flux is reconnected at that surface compared to that reconnected at the  th surface (i.e., the rational surface at which the mode corotates with the local electron fluid). The previous equation can be substituted back into Equation (14.144) to give
th surface (i.e., the rational surface at which the mode corotates with the local electron fluid). The previous equation can be substituted back into Equation (14.144) to give
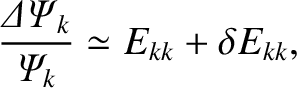 |
(14.148) |
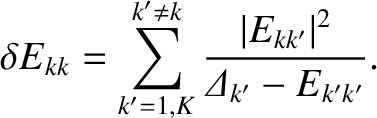 |
(14.149) |
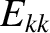 is the tearing stability index of the mode that reconnects magnetic flux at the
is the tearing stability index of the mode that reconnects magnetic flux at the  th rational surface in the limit of
full shielding (i.e.,
th rational surface in the limit of
full shielding (i.e.,
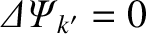 ) at the other rational surfaces, whereas
) at the other rational surfaces, whereas
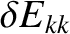 is the correction to this index due to the fact that the
shielding is not actually perfect. Table 14.6 gives the
is the correction to this index due to the fact that the
shielding is not actually perfect. Table 14.6 gives the 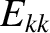 and
and
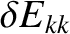 values calculated from the data in Tables 14.2 and 14.4 for the four possible linear
values calculated from the data in Tables 14.2 and 14.4 for the four possible linear  tearing modes in our example tokamak discharge. It can be seen that
tearing modes in our example tokamak discharge. It can be seen that
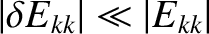 for all modes. In other words,
in all cases, the correction due to residual reconnection at the other rational surfaces is essentially negligible.
for all modes. In other words,
in all cases, the correction due to residual reconnection at the other rational surfaces is essentially negligible.