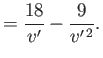Next: Heat Engines
Up: Classical Thermodynamics
Previous: Van der Waals Gas
The difficulty associated with the presence of containing walls can be overcome by
replacing the single-event free-expansion process just described (where this one event must supply the
energy necessary to change the container temperature) with a continuous-flow process (where the temperature
of the walls can adjust itself initially, and remains unchanged after a steady-state has been achieved). We
shall now discuss a specific example of such a process that was first suggested by Joule and Thompson.
Consider a pipe with thermally insulated walls. A porous plug in the pipe provides
a constriction in the flow. A continuous stream of gas flows through the pipe. The
constriction in the flow, due to the presence of the plug, results in a constant pressure difference
being maintained across the plug. Let 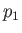 and
and  be the pressure and temperature of the
gas upstream of the plug, respectively, and let
be the pressure and temperature of the
gas upstream of the plug, respectively, and let 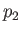 and
and 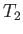 be the downstream pressure and temperature, respectively.
We expect the upstream pressure to exceed the downstream pressure (i.e.,
be the downstream pressure and temperature, respectively.
We expect the upstream pressure to exceed the downstream pressure (i.e., 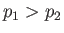 ), otherwise gas would not be
forced through the plug (in the upstream to downstream direction). But, how is the downstream temperature,
), otherwise gas would not be
forced through the plug (in the upstream to downstream direction). But, how is the downstream temperature, 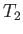 , related to
the upstream temperature,
, related to
the upstream temperature,  ?
?
Consider a mass of gas, 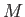 , that flows from the upstream to the downstream side of the plug. In this so-called ``throttling'' process,
the change in internal energy of the mass is
, that flows from the upstream to the downstream side of the plug. In this so-called ``throttling'' process,
the change in internal energy of the mass is
 |
(6.167) |
However, the mass also does work. Let 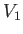 and
and 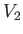 be the upstream and downstream volume of the mass, respectively.
The mass does the work
be the upstream and downstream volume of the mass, respectively.
The mass does the work 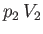 in displacing gas on the downstream side of the plug, whereas the gas on the upstream
side of the plug does the work
in displacing gas on the downstream side of the plug, whereas the gas on the upstream
side of the plug does the work  on the mass. Thus, the net work done by the mass is
on the mass. Thus, the net work done by the mass is
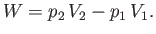 |
(6.168) |
No heat is absorbed by the mass of gas in the throttling process that we have just described. This is not just because the walls of the
pipe are thermally insulated, so that no heat enters from the outside. More importantly, after a steady-state has been
achieved, there is no temperature difference between the walls and the adjacent gas, so there is no heat flow from the
walls to the gas. It follows that
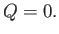 |
(6.169) |
Application of the first law of thermodynamics to the mass of gas yields
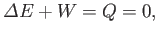 |
(6.170) |
or
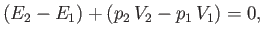 |
(6.171) |
where use has been made of Equations (6.167) and (6.168). Now, the
enthalpy of the gas mass is defined
 |
(6.172) |
(See Section 6.10.) Hence, we deduce that
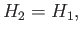 |
(6.173) |
or
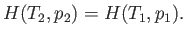 |
(6.174) |
In other words, the gas passes through the porous plug in such a manner that its enthalpy remains
constant.
Suppose that 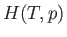 is a known function of
is a known function of  and
and  . In this case, given
. In this case, given  and
and
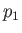 , as well as the downstream pressure,
, as well as the downstream pressure, 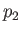 , Equation (6.174) allows the downstream
temperature,
, Equation (6.174) allows the downstream
temperature, 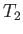 , to be determined. In the case of an ideal gas,
, to be determined. In the case of an ideal gas,
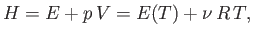 |
(6.175) |
so that 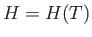 is a function of the temperature only. Thus, Equation (6.174) reduces to
is a function of the temperature only. Thus, Equation (6.174) reduces to
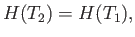 |
(6.176) |
which implies that 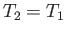 . Thus, the temperature of an ideal gas does not change in a throttling process.
. Thus, the temperature of an ideal gas does not change in a throttling process.
For the case of a real gas, the parameter that controls whether the gas is heated or cooled in a throttling process is
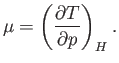 |
(6.177) |
This parameter is known as the Joule-Thompson coefficient. Given that  decreases in a throttling process, a
positive Joule-Thompson coefficient implies that the temperature also decreases, and vice versa. Let us derive a convenient expression
for
decreases in a throttling process, a
positive Joule-Thompson coefficient implies that the temperature also decreases, and vice versa. Let us derive a convenient expression
for  in term of readily measured experimental parameters. Starting from the fundamental thermodynamic relation [see Equation (6.5)]
in term of readily measured experimental parameters. Starting from the fundamental thermodynamic relation [see Equation (6.5)]
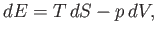 |
(6.178) |
we find that
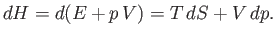 |
(6.179) |
For the case of throttling, 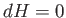 . Thus, we can write
. Thus, we can write
![$\displaystyle 0 = T\left[\left(\frac{\partial S}{\partial T}\right)_pdT + \left(\frac{\partial S}{\partial p}\right)_Tdp\right] +V dp.$](img1160.png) |
(6.180) |
With the aid of Equations (6.119) and (6.121), this becomes
![$\displaystyle 0 = C_p dT +\left[ V - T\left(\frac{\partial V}{\partial T}\right)_p\right]dp.$](img1161.png) |
(6.181) |
Hence,
![$\displaystyle \mu = \left(\frac{dT}{dp}\right)_H =\left. \left[T\left(\frac{\pa...
...\left. \left[T\left(\frac{\partial v}{\partial T}\right)_p-v\right]\right/ c_p,$](img1162.png) |
(6.182) |
where 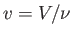 is the molar volume.
is the molar volume.
Figure 6.2:
The solid curve shows the normalized inversion curve of a van der Waals gas. The dashed curve shows the normalized experimental inversion curve of nitrogen gas.
 |
Consider a van der Waals gas.
The
van der Waals equation of state, (6.156), can be written in the reduced form
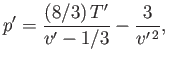 |
(6.183) |
where 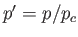 ,
, 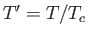 , and
, and 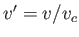 . [See Equations (6.158)-(6.160) and Exercise 13.]
We can also write
. [See Equations (6.158)-(6.160) and Exercise 13.]
We can also write
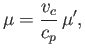 |
(6.184) |
where
 |
(6.185) |
Differentiation of Equation (6.183) yields
 |
(6.186) |
Hence,
![$\displaystyle \mu =\frac{v_c}{3 c_p}\left\{\frac{(27/4) [1-1/(3 v')]^{ 2}-T'}{T'-(27/4) [1-1/(3 v')]^{ 2} [1/(3 v')]}\right\}.$](img1171.png) |
(6.187) |
Thus, we deduce that 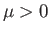 , which is consistent with cooling of the gas in a throttling process, provided that
, which is consistent with cooling of the gas in a throttling process, provided that
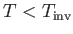 ,
where
,
where
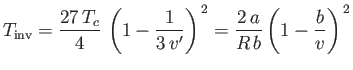 |
(6.188) |
is known as the inversion temperature. Of course, if
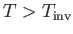 then
then 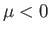 , and the gas is
heated by a throttling process. Let
, and the gas is
heated by a throttling process. Let
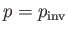 when
when
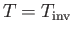 . Equations (6.183) and (6.188)
give
. Equations (6.183) and (6.188)
give
These equations define a curve in the  -
- plane, known as the inversion curve, that is shown in Figure 6.2. (Also shown, for
comparison, is the experimental inversion curve of nitrogen.)
To the left of the curve,
plane, known as the inversion curve, that is shown in Figure 6.2. (Also shown, for
comparison, is the experimental inversion curve of nitrogen.)
To the left of the curve, 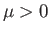 , and the gas is cooled by a throttling process. Conversely, to the right of the curve,
, and the gas is cooled by a throttling process. Conversely, to the right of the curve, 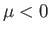 , and
the gas is heated by a throttling process. The maximum possible inversion temperature is
, and
the gas is heated by a throttling process. The maximum possible inversion temperature is
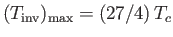 . Thus,
using the data in Table 6.2, we would predict that the maximum inversion temperatures of helium, hydrogen, nitrogen, and
oxygen are 35K, 224K, 852K, and 1044K, respectively. In fact, the experimentally determined maximum inversion
temperatures are 34K, 202K, 625K, and 760K, respectively. Thus, our estimate is fairly accurate in the case of helium, but
becomes increasingly less accurate as the atomic weight of the gas increases. This is merely a deficiency in the van der Waals model.
. Thus,
using the data in Table 6.2, we would predict that the maximum inversion temperatures of helium, hydrogen, nitrogen, and
oxygen are 35K, 224K, 852K, and 1044K, respectively. In fact, the experimentally determined maximum inversion
temperatures are 34K, 202K, 625K, and 760K, respectively. Thus, our estimate is fairly accurate in the case of helium, but
becomes increasingly less accurate as the atomic weight of the gas increases. This is merely a deficiency in the van der Waals model.
The so-called Joule-Thompson throttling process, just described, can be used to cool nitrogen and oxygen to very low
temperatures, starting from room temperature, because the maximum inversion temperatures of these
two gases both exceed room temperature. On the other hand, an attempt to cool helium gas
starting from room temperature would result in an increase, rather than a decrease, in the gas
temperature (because room temperature exceeds the maximum inversion temperature). Thus,
in order to use the Joule-Thompson process to cool helium gas to very low temperatures, it
is first necessary to pre-cool the gas to a temperature that is less than 34K. This can be achieved
using liquid hydrogen.



Next: Heat Engines
Up: Classical Thermodynamics
Previous: Van der Waals Gas
Richard Fitzpatrick
2016-01-25
![]() and
and ![]() be the pressure and temperature of the
gas upstream of the plug, respectively, and let
be the pressure and temperature of the
gas upstream of the plug, respectively, and let ![]() and
and ![]() be the downstream pressure and temperature, respectively.
We expect the upstream pressure to exceed the downstream pressure (i.e.,
be the downstream pressure and temperature, respectively.
We expect the upstream pressure to exceed the downstream pressure (i.e., ![]() ), otherwise gas would not be
forced through the plug (in the upstream to downstream direction). But, how is the downstream temperature,
), otherwise gas would not be
forced through the plug (in the upstream to downstream direction). But, how is the downstream temperature, ![]() , related to
the upstream temperature,
, related to
the upstream temperature, ![]() ?
?
![]() , that flows from the upstream to the downstream side of the plug. In this so-called ``throttling'' process,
the change in internal energy of the mass is
, that flows from the upstream to the downstream side of the plug. In this so-called ``throttling'' process,
the change in internal energy of the mass is
![]() is a known function of
is a known function of ![]() and
and ![]() . In this case, given
. In this case, given ![]() and
and
![]() , as well as the downstream pressure,
, as well as the downstream pressure, ![]() , Equation (6.174) allows the downstream
temperature,
, Equation (6.174) allows the downstream
temperature, ![]() , to be determined. In the case of an ideal gas,
, to be determined. In the case of an ideal gas,
![$\displaystyle 0 = T\left[\left(\frac{\partial S}{\partial T}\right)_pdT + \left(\frac{\partial S}{\partial p}\right)_Tdp\right] +V dp.$](img1160.png)
![$\displaystyle 0 = C_p dT +\left[ V - T\left(\frac{\partial V}{\partial T}\right)_p\right]dp.$](img1161.png)
![$\displaystyle \mu = \left(\frac{dT}{dp}\right)_H =\left. \left[T\left(\frac{\pa...
...\left. \left[T\left(\frac{\partial v}{\partial T}\right)_p-v\right]\right/ c_p,$](img1162.png)



![$\displaystyle \mu =\frac{v_c}{3 c_p}\left\{\frac{(27/4) [1-1/(3 v')]^{ 2}-T'}{T'-(27/4) [1-1/(3 v')]^{ 2} [1/(3 v')]}\right\}.$](img1171.png)