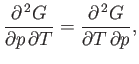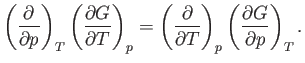

Next: General Relation Between Specific
Up: Classical Thermodynamics
Previous: Helmholtz Free Energy
Suppose, finally, that 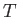 and
and 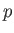 are the are the two independent parameters that specify the system.
Because
are the are the two independent parameters that specify the system.
Because
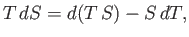 |
(6.110) |
we can rewrite Equation (6.91) in the form
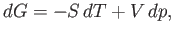 |
(6.111) |
where
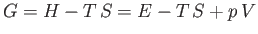 |
(6.112) |
is termed the Gibbs free energy.
Proceeding as before, we write
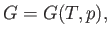 |
(6.113) |
which implies that
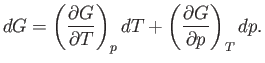 |
(6.114) |
Comparison of Equations (6.111) and (6.114) yields
We also know that
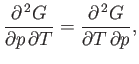 |
(6.117) |
or
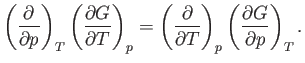 |
(6.118) |
Thus, it follows from Equations (6.115) and (6.116) that
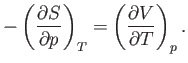 |
(6.119) |
Equations (6.89), (6.99), (6.109), and (6.119) are known collectively
as Maxwell relations.


Next: General Relation Between Specific
Up: Classical Thermodynamics
Previous: Helmholtz Free Energy
Richard Fitzpatrick
2016-01-25