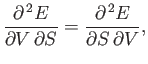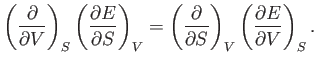

Next: Enthalpy
Up: Classical Thermodynamics
Previous: Adiabatic Atmosphere
Equation (6.5) can be rearranged to give
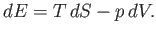 |
(6.82) |
This equation shows how the internal energy, 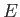 , depends on independent
variations of the entropy,
, depends on independent
variations of the entropy, 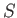 , and the volume,
, and the volume, 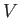 . If
. If 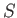 and
and
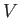 are considered to be the two independent parameters that specify the system then
are considered to be the two independent parameters that specify the system then
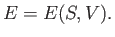 |
(6.83) |
It immediately follows that
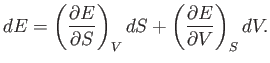 |
(6.84) |
Now, Equations (6.82) and (6.84) must be equivalent for all possible values of
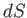 and
and 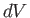 . Hence, we deduce that
. Hence, we deduce that
We also know that
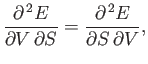 |
(6.87) |
or
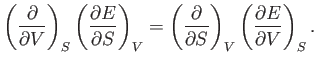 |
(6.88) |
In fact, this is a necessary condition for 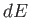 in Equation (6.84) to be an exact differential. (See Section 4.5.)
It follows from Equations (6.85) and (6.86) that
in Equation (6.84) to be an exact differential. (See Section 4.5.)
It follows from Equations (6.85) and (6.86) that
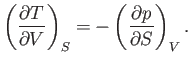 |
(6.89) |


Next: Enthalpy
Up: Classical Thermodynamics
Previous: Adiabatic Atmosphere
Richard Fitzpatrick
2016-01-25