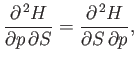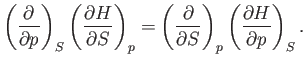

Next: Helmholtz Free Energy
Up: Classical Thermodynamics
Previous: Internal Energy
Enthalpy
The analysis in the previous section is based on the premise that 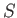 and
and 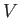 are the two independent parameters that specify the system.
Suppose, however, that we choose
are the two independent parameters that specify the system.
Suppose, however, that we choose 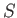 and
and 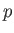 to be the two independent parameters. Because
to be the two independent parameters. Because
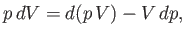 |
(6.90) |
we can rewrite Equation (6.82) in the form
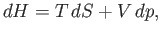 |
(6.91) |
where
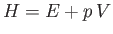 |
(6.92) |
is termed the enthalpy. The name is derived from the Greek enthalpein, which means to ``to warm in."
The analysis now proceeds in an analogous manner to that in the preceding section. First, we
write
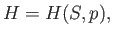 |
(6.93) |
which implies that
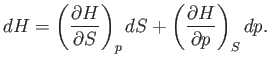 |
(6.94) |
Comparison of Equations (6.91) and (6.94) yields
We also know that
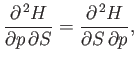 |
(6.97) |
or
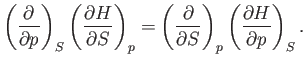 |
(6.98) |
Thus, it follows from Equations (6.95) and (6.96) that
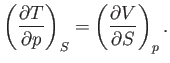 |
(6.99) |


Next: Helmholtz Free Energy
Up: Classical Thermodynamics
Previous: Internal Energy
Richard Fitzpatrick
2016-01-25