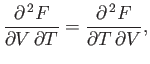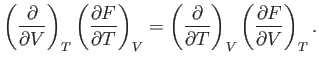

Next: Gibbs Free Energy
Up: Classical Thermodynamics
Previous: Enthalpy
Suppose that 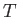 and
and 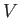 are the are the two independent parameters that specify the system.
Because
are the are the two independent parameters that specify the system.
Because
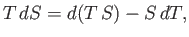 |
(6.100) |
we can rewrite Equation (6.82) in the form
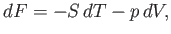 |
(6.101) |
where
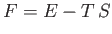 |
(6.102) |
is termed the Helmholtz free energy.
Proceeding as before, we write
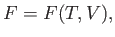 |
(6.103) |
which implies that
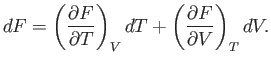 |
(6.104) |
Comparison of Equations (6.101) and (6.104) yields
We also know that
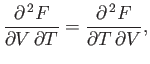 |
(6.107) |
or
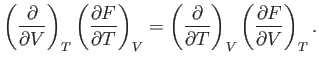 |
(6.108) |
Thus, it follows from Equations (6.105) and (6.106) that
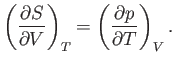 |
(6.109) |


Next: Gibbs Free Energy
Up: Classical Thermodynamics
Previous: Enthalpy
Richard Fitzpatrick
2016-01-25