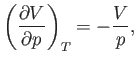Next: Free Expansion of Gas
Up: Classical Thermodynamics
Previous: Gibbs Free Energy
Consider a general homogeneous substance (not necessarily a gas) whose volume,  , is the
only relevant external parameter. Let us find the general relationship between this substance's
molar specific heat at constant volume,
, is the
only relevant external parameter. Let us find the general relationship between this substance's
molar specific heat at constant volume, 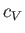 , and its molar specific heat at constant pressure,
, and its molar specific heat at constant pressure, 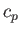 .
.
The heat capacity at constant volume is given by
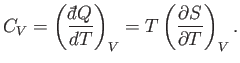 |
(6.120) |
Likewise, the heat capacity at constant pressure is written
 |
(6.121) |
Experimentally, the parameters that are most easily controlled are the temperature,  , and the pressure,
, and the pressure,  .
Let us consider these as the independent variables. Thus,
.
Let us consider these as the independent variables. Thus,  , which implies that
, which implies that
![$\displaystyle {\mathchar'26\mkern-11mud}Q = T dS = T\left[\left(\frac{\partial...
...\partial T}\right)_p dT +\left(\frac{\partial S}{\partial p}\right)_T dp\right]$](img1051.png) |
(6.122) |
in an infinitesimal quasi-static process in which an amount of heat
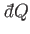 is absorbed.
It follows from Equation (6.121) that
is absorbed.
It follows from Equation (6.121) that
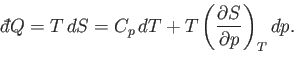 |
(6.123) |
Suppose that 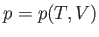 . The previous equation can be written
. The previous equation can be written
![$\displaystyle {\mathchar'26\mkern-11mud}Q = T dS = C_p dT + T\left(\frac{\par...
...partial T}\right)_V dT +\left(\frac{\partial p}{\partial V}\right)_T dV\right].$](img1054.png) |
(6.124) |
At constant volume, 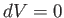 . Hence, Equation (6.120) gives
. Hence, Equation (6.120) gives
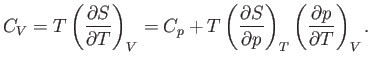 |
(6.125) |
This is the general relationship between 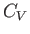 and
and  . Unfortunately, it contains quantities on the right-hand side that are not
readily measurable.
. Unfortunately, it contains quantities on the right-hand side that are not
readily measurable.
Consider
 . According to the Maxwell relation (6.119),
. According to the Maxwell relation (6.119),
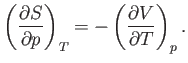 |
(6.126) |
Now, the quantity
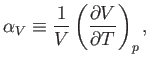 |
(6.127) |
which is known as the volume coefficient of expansion, is easily measured experimentally. Hence, it is convenient to make the
substitution
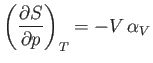 |
(6.128) |
in Equation (6.125).
Consider the quantity
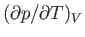 . Writing
. Writing 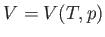 , we obtain
, we obtain
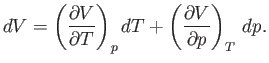 |
(6.129) |
At constant volume, 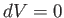 , so we obtain
, so we obtain
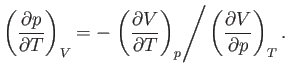 |
(6.130) |
The (usually positive) quantity
 |
(6.131) |
which is known as the isothermal compressibility, is easily measured experimentally. Hence, it is convenient to make
the substitution
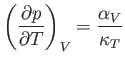 |
(6.132) |
in Equation (6.125). It follows that
 |
(6.133) |
and
 |
(6.134) |
where 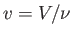 is the molar volume.
is the molar volume.
As an example, consider an ideal gas, for which
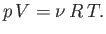 |
(6.135) |
At constant  , we have
, we have
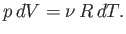 |
(6.136) |
Hence,
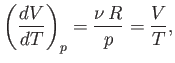 |
(6.137) |
and the expansion coefficient defined in Equation (6.127) becomes
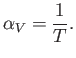 |
(6.138) |
At constant  , we have
, we have
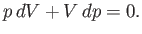 |
(6.139) |
Hence,
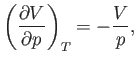 |
(6.140) |
and the compressibility defined in Equation (6.131) becomes
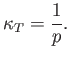 |
(6.141) |
Finally, the molar volume of an ideal gas is
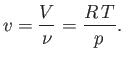 |
(6.142) |
Hence, Equations (6.134), (6.138), (6.141), and (6.142) yield
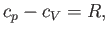 |
(6.143) |
which is identical to Equation (6.39).



Next: Free Expansion of Gas
Up: Classical Thermodynamics
Previous: Gibbs Free Energy
Richard Fitzpatrick
2016-01-25
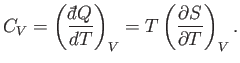
![]() , and the pressure,
, and the pressure, ![]() .
Let us consider these as the independent variables. Thus,
.
Let us consider these as the independent variables. Thus, ![]() , which implies that
, which implies that
![$\displaystyle {\mathchar'26\mkern-11mud}Q = T dS = T\left[\left(\frac{\partial...
...\partial T}\right)_p dT +\left(\frac{\partial S}{\partial p}\right)_T dp\right]$](img1051.png)
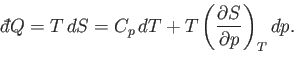
![$\displaystyle {\mathchar'26\mkern-11mud}Q = T dS = C_p dT + T\left(\frac{\par...
...partial T}\right)_V dT +\left(\frac{\partial p}{\partial V}\right)_T dV\right].$](img1054.png)
![]() . According to the Maxwell relation (6.119),
. According to the Maxwell relation (6.119),
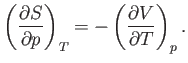
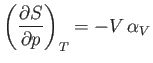
![]() . Writing
. Writing ![]() , we obtain
, we obtain
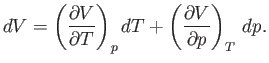
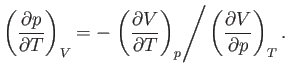

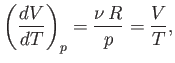
![]() , we have
, we have