


Next: Joule-Thompson Throttling
Up: Classical Thermodynamics
Previous: Free Expansion of Gas
Van der Waals Gas
Consider a non-ideal gas whose equation of state takes the form
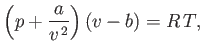 |
(6.156) |
where 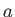 and
and 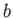 are positive constants. (See Section 8.11.) Such a gas is known as a van der Waals gas. The previous approximate equation of
state attempts to take into account the existence of long-range attractive forces between molecules in real gases, as well as the finite
volume occupied by the molecules themselves. The attractive forces gives rise to a slight compression of the gas
(relative to an ideal gas)--the term
are positive constants. (See Section 8.11.) Such a gas is known as a van der Waals gas. The previous approximate equation of
state attempts to take into account the existence of long-range attractive forces between molecules in real gases, as well as the finite
volume occupied by the molecules themselves. The attractive forces gives rise to a slight compression of the gas
(relative to an ideal gas)--the term 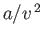 represents this additional positive pressure. The parameter
represents this additional positive pressure. The parameter 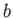 is the
volume occupied by a mole of gas molecules. Thus,
is the
volume occupied by a mole of gas molecules. Thus,
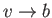 as
as
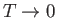 . Of course, in the
limit
. Of course, in the
limit
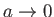 and
and
 , the van der Waals equation of state reduces to the ideal
gas equation of state.
, the van der Waals equation of state reduces to the ideal
gas equation of state.
Table 6.2:
Critical pressures and temperatures, and derived van der Waals parameters, for common gases.
| Gas |
Symbol |
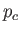 (bar)
(bar) |
 (K)
(K) |
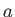 (SI)
(SI) |
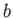 (SI)
(SI) |
| |
|
|
|
|
|
| |
|
|
|
|
|
| Helium |
He |
2.27 |
5.19 |

|
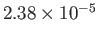
|
| Hydrogen |
H |
13.0 |
33.2 |

|
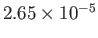
|
| Nitrogen |
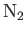
|
33.9 |
126.2 |

|
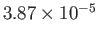
|
| Oxygen |
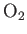
|
50.5 |
154.6 |
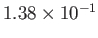
|
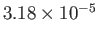
|
|
The van der Waals equation of state can be written
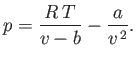 |
(6.157) |
At fixed temperature, the previous equation yields 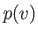 curves that exhibit a maximum and a minimum at
two points where
curves that exhibit a maximum and a minimum at
two points where
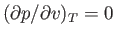 . At a particular temperature, the maximum and minimum
coalesce into a single inflection point where
. At a particular temperature, the maximum and minimum
coalesce into a single inflection point where
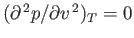 , in addition to
, in addition to
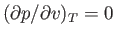 . This point is called the critical point, and its
temperature, pressure, and molar volume are denoted
. This point is called the critical point, and its
temperature, pressure, and molar volume are denoted  ,
, 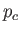 , and
, and  , respectively.
It is readily demonstrated that
, respectively.
It is readily demonstrated that
(See Exercise 13.) The critical temperature,  , and the critical pressure,
, and the critical pressure, 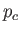 , of a substance
are easily determined experimentally, because they turn out to be the maximum temperature and pressure, respectively, at which distinct
liquid and gas phases exist. (See Section 9.10.) This allows a determination of the constants
, of a substance
are easily determined experimentally, because they turn out to be the maximum temperature and pressure, respectively, at which distinct
liquid and gas phases exist. (See Section 9.10.) This allows a determination of the constants 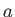 and
and 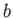 in the van der Waals equation of state.
In fact,
in the van der Waals equation of state.
In fact,
Table 6.2 shows the experimentally measured critical pressures and temperatures, as well as the derived van der Waal parameters, for
some common gases.
Let us calculate the Joule coefficient for a van der Waals gas.
It follows from Equation (6.156) that
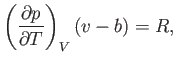 |
(6.163) |
which implies that
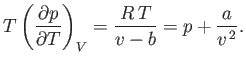 |
(6.164) |
Substitution into Equation (6.155) gives
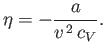 |
(6.165) |
Thus, the Joule coefficient for a van der Waals gas is negative. This implies that the temperature of the gas
always decreases as it undergoes free expansion. Of course, this temperature decrease is a consequence of the
work done in overcoming the inter-molecular attractive forces. Over a relatively small temperature range, 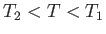 , any
possible temperature dependence of
, any
possible temperature dependence of  is negligibly small. Thus,
is negligibly small. Thus, 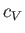 can be regarded as essentially constant, and Equations (6.149)
and (6.165) yield
can be regarded as essentially constant, and Equations (6.149)
and (6.165) yield
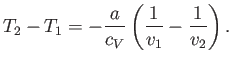 |
(6.166) |
For an expansion, where 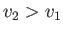 , this equation confirms that
, this equation confirms that 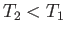 . In other words, the temperature of non-ideal gas that undergoes free expansion
is reduced.
. In other words, the temperature of non-ideal gas that undergoes free expansion
is reduced.
In principle, it appears that the free expansion of a gas could provide a method of cooling the gas to
low temperatures. In practice, a substantial difficulty arises because of the appreciable heat capacity,
 , of the container. Because the container's internal energy changes by an amount
, of the container. Because the container's internal energy changes by an amount
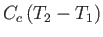 , the molar heat capacity,
, the molar heat capacity, 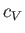 , in Equation (6.166),
must be replaced by the total molar heat capacity,
, in Equation (6.166),
must be replaced by the total molar heat capacity,
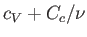 . Given that the heat capacity of the container is generally much greater than that of the
gas (i.e.,
. Given that the heat capacity of the container is generally much greater than that of the
gas (i.e.,
 ), it follows that the actual temperature reduction is much smaller than that predicted by Equation (6.166).
), it follows that the actual temperature reduction is much smaller than that predicted by Equation (6.166).



Next: Joule-Thompson Throttling
Up: Classical Thermodynamics
Previous: Free Expansion of Gas
Richard Fitzpatrick
2016-01-25
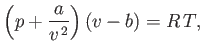
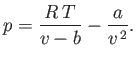
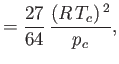
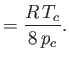
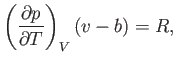
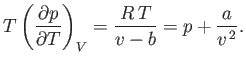
![]() , of the container. Because the container's internal energy changes by an amount
, of the container. Because the container's internal energy changes by an amount
![]() , the molar heat capacity,
, the molar heat capacity, ![]() , in Equation (6.166),
must be replaced by the total molar heat capacity,
, in Equation (6.166),
must be replaced by the total molar heat capacity,
![]() . Given that the heat capacity of the container is generally much greater than that of the
gas (i.e.,
. Given that the heat capacity of the container is generally much greater than that of the
gas (i.e.,
![]() ), it follows that the actual temperature reduction is much smaller than that predicted by Equation (6.166).
), it follows that the actual temperature reduction is much smaller than that predicted by Equation (6.166).