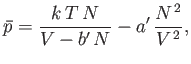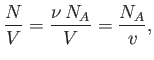Next: Planck Radiation Law
Up: Quantum Statistics
Previous: Quantum-Mechanical Treatment of Ideal
Derivation of van der Waals Equation of State
We shall now extend the analysis of the previous section to derive an approximate equation of state for a non-ideal gas.
Let us focus attention on a single molecule. It seems reasonable to suppose that this molecule
moves in an effective potential,
 , due to all the other molecules in the gas (which
are assumed to remain unaffected by the presence of the molecule under consideration). Under these circumstances, the
partition function of the gas reduces to that of
, due to all the other molecules in the gas (which
are assumed to remain unaffected by the presence of the molecule under consideration). Under these circumstances, the
partition function of the gas reduces to that of  independent particles, each with a kinetic energy
independent particles, each with a kinetic energy
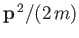 ,
and a potential energy
,
and a potential energy 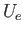 .
.
Proceeding classically (except that the molecules are treated as
indistinguishable, and the arbitrary parameter  is replaced by Planck's constant), we obtain
is replaced by Planck's constant), we obtain
![$\displaystyle Z =\frac{1}{N!}\left[\int\int {\rm e}^{-\beta (p^{ 2}/2 m+U_e)} \frac{d^{ 3}{\bf r} d^{ 3}{\bf p}}{h^{ 3}}\right]^{ N}.$](img2121.png) |
(8.85) |
(See Sections 7.7 and 8.10.)
Thus,
![$\displaystyle Z =\frac{1}{N!}\left[\int \exp\left(\frac{-\beta p_x^{ 2}}{2 m...
...m}\right)\frac{dp_z}{h}\int {\rm e}^{-\beta U_e} d^{ 3}{\bf r}\right]^{ N},$](img2122.png) |
(8.86) |
which yields
![$\displaystyle Z = \frac{1}{N!}\left[\left(\frac{2\pi m}{\beta h^{ 2}}\right)^{3/2}\int {\rm e}^{-\beta U_e} d^{ 3}{\bf r}\right]^{ N}.$](img2123.png) |
(8.87) |
(See Exercise 2.)
The remaining integral extends over the volume,  , of the container. To make further progress, we note that there are
regions in which
, of the container. To make further progress, we note that there are
regions in which
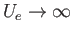 because of the strong repulsion between molecules when they approach one another too closely. Thus, the integrand vanishes
in these regions, which are assumed to have a total volume
because of the strong repulsion between molecules when they approach one another too closely. Thus, the integrand vanishes
in these regions, which are assumed to have a total volume 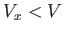 . In the remaining volume,
. In the remaining volume, 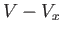 , where
, where 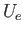 is assumed to vary relatively slowly with inter-molecular separation, we shall replace
is assumed to vary relatively slowly with inter-molecular separation, we shall replace 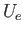 by some effective constant
average value,
by some effective constant
average value,
 . Thus, the previous equation becomes
. Thus, the previous equation becomes
![$\displaystyle Z = \frac{1}{N!}\left[\left(\frac{2\pi m}{h^{ 2} \beta}\right)^{3/2}(V-V_x) {\rm e}^{-\beta \overline{U}_e}\right]^{ N}.$](img2128.png) |
(8.88) |
It remains to estimate the values of the parameters
 and
and  . The total mean potential energy of the
molecules is
. The total mean potential energy of the
molecules is
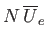 . But, because there are
. But, because there are
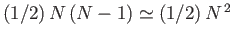 pairs of molecules in the gas, it follows
that the total mean potential energy is also
pairs of molecules in the gas, it follows
that the total mean potential energy is also
 , where
, where 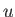 is the potential energy of interaction between a given pair of
molecules. Equating the different expressions for the total mean potential energy of the gas, we obtain
is the potential energy of interaction between a given pair of
molecules. Equating the different expressions for the total mean potential energy of the gas, we obtain
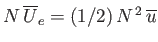 , or
, or
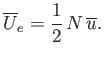 |
(8.89) |
To estimate the mean potential energy,  , between a pair of molecules, let us make the simplistic assumption that the interaction potential takes the form
, between a pair of molecules, let us make the simplistic assumption that the interaction potential takes the form
![$\displaystyle u(R)=\left\{ \begin{array}{lll} \infty &\mbox{\hspace{1cm}}& R<R_0\ [0.5ex] -u_0\left(R_0/R\right)^s&&R>R_0\end{array} \right.,$](img2135.png) |
(8.90) |
where 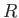 is separation between the molecular centers,
is separation between the molecular centers,  , and
, and 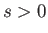 . Thus, the molecules act as weakly-attracting hard
spheres of radius
. Thus, the molecules act as weakly-attracting hard
spheres of radius
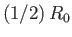 . The choice of exponent
. The choice of exponent  is usually the most appropriate. (See Exercise 8.) Concentrating attention on a particular molecule,
and making the crudest possible approximation,
we shall say that another molecule is equally likely to be anywhere in the container that is a distance
is usually the most appropriate. (See Exercise 8.) Concentrating attention on a particular molecule,
and making the crudest possible approximation,
we shall say that another molecule is equally likely to be anywhere in the container that is a distance 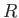 greater than
greater than 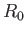 from the given molecule.
Thus, the probability of the distance lying between
from the given molecule.
Thus, the probability of the distance lying between 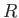 and
and 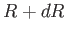 is
is
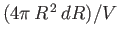 , and
, and
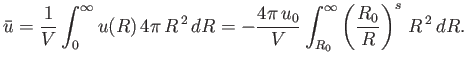 |
(8.91) |
Let us assume that 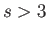 : in other words, the potential
: in other words, the potential 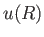 falls off sufficiently rapidly for the previous integral to converge properly.
Thus, Equation (8.89) becomes
falls off sufficiently rapidly for the previous integral to converge properly.
Thus, Equation (8.89) becomes
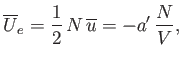 |
(8.92) |
where
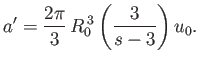 |
(8.93) |
By Equation (8.90), the distance of closest approach between molecules is 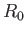 . Thus, in each encounter between
a pair of molecules, there is a volume excluded to one molecule, by virtue of the presence of the other molecule, that is
equal to the volume of a sphere of radius
. Thus, in each encounter between
a pair of molecules, there is a volume excluded to one molecule, by virtue of the presence of the other molecule, that is
equal to the volume of a sphere of radius 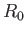 . Because there are
. Because there are
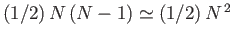 pairs of molecules, the
total excluded volume is
pairs of molecules, the
total excluded volume is
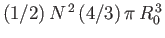 . But, for the sake of consistency, this volume must be equal to
. But, for the sake of consistency, this volume must be equal to
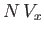 , because
, because  was understood to be the excluded volume per molecule. Thus, it follows that
was understood to be the excluded volume per molecule. Thus, it follows that
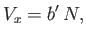 |
(8.94) |
where
![$\displaystyle b'=\frac{2\pi}{3} R_0^{ 3} = 4\left[\frac{4\pi}{3}\left(\frac{R_0}{2}\right)^3\right]$](img2151.png) |
(8.95) |
is four times the volume of a hard-sphere molecule.
This completes our crude evaluation of the partition function. The equation of state of the gas is given by
![$\displaystyle \bar{p} =\frac{1}{\beta} \frac{\partial \ln Z}{\partial V} =\fra...
...\frac{\partial}{\partial V}\left[N \ln(V-V_x)-N \beta \overline{U}_e\right].$](img2152.png) |
(8.96) |
Making use of Equations (8.92) and (8.94), we obtain
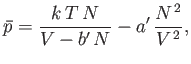 |
(8.97) |
or
 |
(8.98) |
Now,
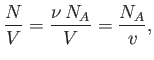 |
(8.99) |
where 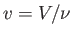 is the molar volume. Thus, our approximate equation of state becomes
is the molar volume. Thus, our approximate equation of state becomes
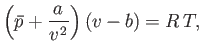 |
(8.100) |
where
Of course, Equation (8.100) is identical to the well-known van der Waals equation of state. (See Section 6.15.)
Our analysis allows us to relate the constants, 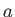 and
and 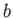 , appearing in this equation of state, to the inter-molecular potential.
, appearing in this equation of state, to the inter-molecular potential.



Next: Planck Radiation Law
Up: Quantum Statistics
Previous: Quantum-Mechanical Treatment of Ideal
Richard Fitzpatrick
2016-01-25
![]() is replaced by Planck's constant), we obtain
is replaced by Planck's constant), we obtain
![$\displaystyle Z =\frac{1}{N!}\left[\int\int {\rm e}^{-\beta (p^{ 2}/2 m+U_e)} \frac{d^{ 3}{\bf r} d^{ 3}{\bf p}}{h^{ 3}}\right]^{ N}.$](img2121.png)
![$\displaystyle Z =\frac{1}{N!}\left[\int \exp\left(\frac{-\beta p_x^{ 2}}{2 m...
...m}\right)\frac{dp_z}{h}\int {\rm e}^{-\beta U_e} d^{ 3}{\bf r}\right]^{ N},$](img2122.png)
![$\displaystyle Z = \frac{1}{N!}\left[\left(\frac{2\pi m}{\beta h^{ 2}}\right)^{3/2}\int {\rm e}^{-\beta U_e} d^{ 3}{\bf r}\right]^{ N}.$](img2123.png)
![]() , of the container. To make further progress, we note that there are
regions in which
, of the container. To make further progress, we note that there are
regions in which
![]() because of the strong repulsion between molecules when they approach one another too closely. Thus, the integrand vanishes
in these regions, which are assumed to have a total volume
because of the strong repulsion between molecules when they approach one another too closely. Thus, the integrand vanishes
in these regions, which are assumed to have a total volume ![]() . In the remaining volume,
. In the remaining volume, ![]() , where
, where ![]() is assumed to vary relatively slowly with inter-molecular separation, we shall replace
is assumed to vary relatively slowly with inter-molecular separation, we shall replace ![]() by some effective constant
average value,
by some effective constant
average value,
![]() . Thus, the previous equation becomes
. Thus, the previous equation becomes
![$\displaystyle Z = \frac{1}{N!}\left[\left(\frac{2\pi m}{h^{ 2} \beta}\right)^{3/2}(V-V_x) {\rm e}^{-\beta \overline{U}_e}\right]^{ N}.$](img2128.png)
![]() and
and ![]() . The total mean potential energy of the
molecules is
. The total mean potential energy of the
molecules is
![]() . But, because there are
. But, because there are
![]() pairs of molecules in the gas, it follows
that the total mean potential energy is also
pairs of molecules in the gas, it follows
that the total mean potential energy is also
![]() , where
, where ![]() is the potential energy of interaction between a given pair of
molecules. Equating the different expressions for the total mean potential energy of the gas, we obtain
is the potential energy of interaction between a given pair of
molecules. Equating the different expressions for the total mean potential energy of the gas, we obtain
![]() , or
, or
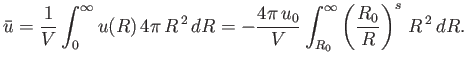
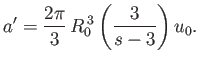
![]() . Thus, in each encounter between
a pair of molecules, there is a volume excluded to one molecule, by virtue of the presence of the other molecule, that is
equal to the volume of a sphere of radius
. Thus, in each encounter between
a pair of molecules, there is a volume excluded to one molecule, by virtue of the presence of the other molecule, that is
equal to the volume of a sphere of radius ![]() . Because there are
. Because there are
![]() pairs of molecules, the
total excluded volume is
pairs of molecules, the
total excluded volume is
![]() . But, for the sake of consistency, this volume must be equal to
. But, for the sake of consistency, this volume must be equal to
![]() , because
, because ![]() was understood to be the excluded volume per molecule. Thus, it follows that
was understood to be the excluded volume per molecule. Thus, it follows that
![$\displaystyle b'=\frac{2\pi}{3} R_0^{ 3} = 4\left[\frac{4\pi}{3}\left(\frac{R_0}{2}\right)^3\right]$](img2151.png)
![$\displaystyle \bar{p} =\frac{1}{\beta} \frac{\partial \ln Z}{\partial V} =\fra...
...\frac{\partial}{\partial V}\left[N \ln(V-V_x)-N \beta \overline{U}_e\right].$](img2152.png)