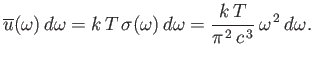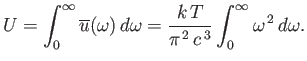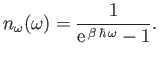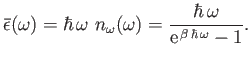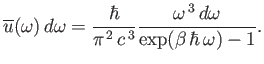Next: Black-Body Radiation
Up: Quantum Statistics
Previous: Derivation of van der
Planck Radiation Law
Let us now consider the application of statistical thermodynamics to electromagnetic
radiation. According to Maxwell's theory, an electromagnetic wave is a coupled
self-sustaining
oscillation of electric and magnetic fields that propagates though a vacuum at
the speed of light,
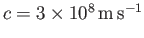 . The electric
component of the wave can be written
. The electric
component of the wave can be written
![$\displaystyle {\bf E} = {\bf E}_0 \exp[ {\rm i} ({\bf k}\!\cdot \!{\bf r} - \omega t)],$](img2160.png) |
(8.103) |
where 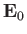 is a constant,
is a constant, 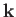 is the wavevector that determines
the wavelength and direction of propagation of the wave, and
is the wavevector that determines
the wavelength and direction of propagation of the wave, and 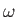 is
the angular frequency. The dispersion relation
is
the angular frequency. The dispersion relation
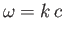 |
(8.104) |
ensures that the wave propagates at the speed of light. Note that this dispersion
relation is very similar to that of sound waves in solids. [See Equation (7.177).]
Electromagnetic waves always propagate in the direction perpendicular to the
coupled electric and magnetic fields (i.e.,
electromagnetic waves are transverse waves).
This means that
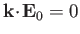 . Thus, once
. Thus, once 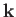 is specified,
there are only two possible
independent
directions for the electric field.
These correspond to the two independent polarizations of electromagnetic waves.
is specified,
there are only two possible
independent
directions for the electric field.
These correspond to the two independent polarizations of electromagnetic waves.
Consider an enclosure whose walls are maintained at fixed
temperature  . What is the nature of the
steady-state electromagnetic radiation inside
the enclosure? Suppose that the enclosure is a parallelepiped with
sides of lengths
. What is the nature of the
steady-state electromagnetic radiation inside
the enclosure? Suppose that the enclosure is a parallelepiped with
sides of lengths 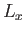 ,
, 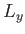 , and
, and 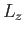 . Alternatively (and more conveniently), suppose that the
radiation field inside the enclosure is periodic in the
. Alternatively (and more conveniently), suppose that the
radiation field inside the enclosure is periodic in the 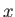 -,
-, 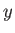 -, and
-, and 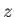 -directions,
with periodicity lengths
-directions,
with periodicity lengths 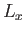 ,
, 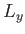 , and
, and 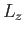 , respectively. As long as the
smallest of these lengths,
, respectively. As long as the
smallest of these lengths, 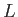 , say, is much greater than the longest wavelength
of interest in the problem,
, say, is much greater than the longest wavelength
of interest in the problem,
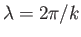 , then these assumptions should not
significantly
affect the nature of the radiation inside the enclosure. We find, just as in
our earlier discussion of sound waves (see Section 7.14), that the periodicity constraints ensure that
there are only a discrete set of allowed wavevectors (i.e., a discrete
set of allowed modes of oscillation of the electromagnetic field inside the
enclosure).
Let
, then these assumptions should not
significantly
affect the nature of the radiation inside the enclosure. We find, just as in
our earlier discussion of sound waves (see Section 7.14), that the periodicity constraints ensure that
there are only a discrete set of allowed wavevectors (i.e., a discrete
set of allowed modes of oscillation of the electromagnetic field inside the
enclosure).
Let
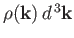 be the number of allowed modes per unit volume
with wavevectors in the range
be the number of allowed modes per unit volume
with wavevectors in the range 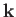 to
to
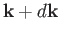 . We know,
by analogy with
Equation (7.183), that
. We know,
by analogy with
Equation (7.183), that
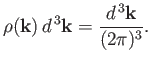 |
(8.105) |
The number of modes per unit volume for which the magnitude of
the wavevector lies in the range 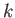 to
to 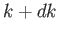 is just the density of modes,
is just the density of modes,
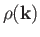 ,
multiplied by the ``volume'' in
,
multiplied by the ``volume'' in 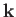 -space of the spherical shell
lying between radii
-space of the spherical shell
lying between radii 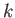 and
and 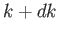 . Thus,
. Thus,
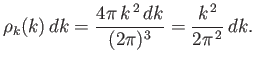 |
(8.106) |
Finally, the number of modes per unit volume whose frequencies lie between
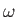 and
and
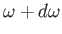 is, by Equation (8.104),
is, by Equation (8.104),
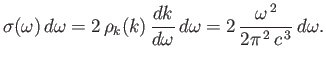 |
(8.107) |
Here, the additional
factor 2 is to take account of the two independent polarizations
of the electromagnetic field for a given wavevector, 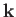 .
.
Let us consider the situation classically. By analogy with sound waves, we can treat
each allowable mode of oscillation of the electromagnetic field as an independent
harmonic oscillator. According to the equipartition theorem
(see Section 7.10), each mode possesses a
mean energy 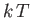 in thermal equilibrium at temperature
in thermal equilibrium at temperature  . In fact,
. In fact,
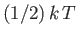 resides with the oscillating electric field, and another
resides with the oscillating electric field, and another
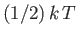 with
the oscillating magnetic field.
Thus,
the classical energy density of electromagnetic radiation (i.e., the
energy per unit volume associated with modes whose frequencies lie in the
range
with
the oscillating magnetic field.
Thus,
the classical energy density of electromagnetic radiation (i.e., the
energy per unit volume associated with modes whose frequencies lie in the
range 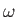 to
to
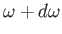 ) is
) is
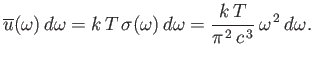 |
(8.108) |
This result is known as the Rayleigh-Jeans radiation law, after Lord Rayleigh
and James Jeans who first proposed it in the late nineteenth century.
According to Debye theory (see Section 7.14),
the energy density of sound waves in a solid is
analogous to the Rayleigh-Jeans law, with one very important difference.
In Debye theory,
there is a cut-off frequency (the Debye frequency) above which
no modes exist. This cut-off comes about because of the discrete nature of
solids (i.e., because solids
are made up of atoms instead of being continuous).
It is, of course,
impossible to have sound waves whose wavelengths are much less than
the inter-atomic spacing.
On the other hand, electromagnetic waves propagate through a vacuum,
which possesses no discrete structure. It follows that
there is no cut-off frequency for electromagnetic waves, and so the Rayleigh-Jeans
law holds for all frequencies. This immediately poses a severe problem. The total
classical energy density of electromagnetic radiation is given by
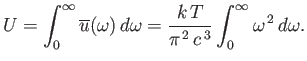 |
(8.109) |
This is an integral that obviously does not converge. Thus, according to classical
physics, the total energy density of electromagnetic radiation inside an enclosed cavity
is infinite. This is clearly an absurd result, and was recognized as such
in the latter half of the nineteenth century. In fact, this prediction
is known as the ultra-violet catastrophe, because the Rayleigh-Jeans
law usually starts to diverge badly from experimental
observations (by over-estimating the amount of radiation) in the
ultra-violet region of the spectrum.
So, how do we obtain a sensible answer? As usual, quantum mechanics comes
to our rescue. According to quantum mechanics,
each allowable mode of oscillation of the
electromagnetic field corresponds to a photon state with energy and
momentum
respectively.
Incidentally, it follows from Equation (8.104) that
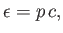 |
(8.112) |
which implies that photons are massless particles that move at the speed of
light.
According to the Planck distribution, (8.39), the mean number of
photons occupying a photon state of frequency 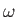 is
is
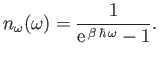 |
(8.113) |
Hence, the mean energy of such a state is given by
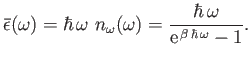 |
(8.114) |
Note that low-frequency states (i.e.,
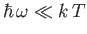 ) behave
classically: that is,
) behave
classically: that is,
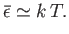 |
(8.115) |
On the other hand, high-frequency states (i.e.,
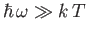 )
are completely ``frozen out'': that is,
)
are completely ``frozen out'': that is,
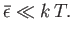 |
(8.116) |
The reason for this is simply that it is very difficult for a thermal
fluctuation to create a photon with an energy greatly in excess of 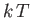 ,
because
,
because 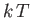 is the characteristic energy associated with such fluctuations.
is the characteristic energy associated with such fluctuations.
According to the previous discussion, the true energy density of
electromagnetic radiation inside an enclosed cavity is written
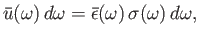 |
(8.117) |
giving
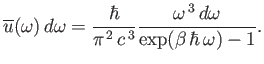 |
(8.118) |
This is famous
result is known as the Planck radiation law.
The Planck law approximates to the
classical Rayleigh-Jeans law for
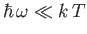 , peaks at about
, peaks at about
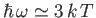 (see Exercise 15), and falls off exponentially for
(see Exercise 15), and falls off exponentially for
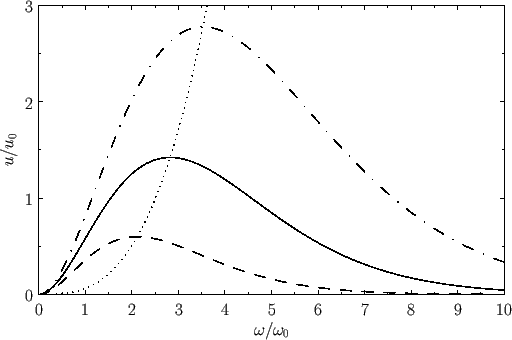
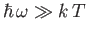 . (See Figure 8.2.)
The exponential fall off at high frequencies ensures that the total energy density
remains finite.
. (See Figure 8.2.)
The exponential fall off at high frequencies ensures that the total energy density
remains finite.
Figure:
The Planck radiation law. Here,
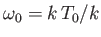 and
and
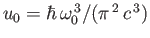 , where
, where 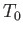 is an arbitrary scale temperature. The dashed, solid, and dash-dotted curves show
is an arbitrary scale temperature. The dashed, solid, and dash-dotted curves show
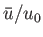 for
for
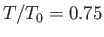 ,
, 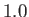 , and
, and
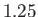 , respectively. The dotted curve shows the locus of the peak emission frequency.
, respectively. The dotted curve shows the locus of the peak emission frequency.
 |



Next: Black-Body Radiation
Up: Quantum Statistics
Previous: Derivation of van der
Richard Fitzpatrick
2016-01-25
![]() . What is the nature of the
steady-state electromagnetic radiation inside
the enclosure? Suppose that the enclosure is a parallelepiped with
sides of lengths
. What is the nature of the
steady-state electromagnetic radiation inside
the enclosure? Suppose that the enclosure is a parallelepiped with
sides of lengths ![]() ,
, ![]() , and
, and ![]() . Alternatively (and more conveniently), suppose that the
radiation field inside the enclosure is periodic in the
. Alternatively (and more conveniently), suppose that the
radiation field inside the enclosure is periodic in the ![]() -,
-, ![]() -, and
-, and ![]() -directions,
with periodicity lengths
-directions,
with periodicity lengths ![]() ,
, ![]() , and
, and ![]() , respectively. As long as the
smallest of these lengths,
, respectively. As long as the
smallest of these lengths, ![]() , say, is much greater than the longest wavelength
of interest in the problem,
, say, is much greater than the longest wavelength
of interest in the problem,
![]() , then these assumptions should not
significantly
affect the nature of the radiation inside the enclosure. We find, just as in
our earlier discussion of sound waves (see Section 7.14), that the periodicity constraints ensure that
there are only a discrete set of allowed wavevectors (i.e., a discrete
set of allowed modes of oscillation of the electromagnetic field inside the
enclosure).
Let
, then these assumptions should not
significantly
affect the nature of the radiation inside the enclosure. We find, just as in
our earlier discussion of sound waves (see Section 7.14), that the periodicity constraints ensure that
there are only a discrete set of allowed wavevectors (i.e., a discrete
set of allowed modes of oscillation of the electromagnetic field inside the
enclosure).
Let
![]() be the number of allowed modes per unit volume
with wavevectors in the range
be the number of allowed modes per unit volume
with wavevectors in the range ![]() to
to
![]() . We know,
by analogy with
Equation (7.183), that
. We know,
by analogy with
Equation (7.183), that
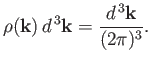
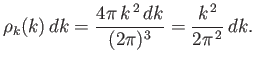
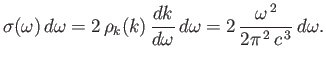
![]() in thermal equilibrium at temperature
in thermal equilibrium at temperature ![]() . In fact,
. In fact,
![]() resides with the oscillating electric field, and another
resides with the oscillating electric field, and another
![]() with
the oscillating magnetic field.
Thus,
the classical energy density of electromagnetic radiation (i.e., the
energy per unit volume associated with modes whose frequencies lie in the
range
with
the oscillating magnetic field.
Thus,
the classical energy density of electromagnetic radiation (i.e., the
energy per unit volume associated with modes whose frequencies lie in the
range ![]() to
to
![]() ) is
) is