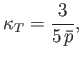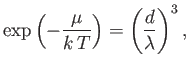Next: Multi-Phase Systems
Up: Quantum Statistics
Previous: Bose-Einstein Condensation
- Let
where  is a non-negative integer. Integrating by parts, demonstrate that
is a non-negative integer. Integrating by parts, demonstrate that
Furthermore, show that
Hence, deduce that
- Let
where  is an integer greater than unity.
Demonstrate that
is an integer greater than unity.
Demonstrate that
where
is a Riemann zeta function.
[Hint:
 , provided that
, provided that  .]
In general, the zeta function must be evaluated numerically. However, it is possible to
prove that
.]
In general, the zeta function must be evaluated numerically. However, it is possible to
prove that
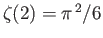 and
and
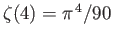 .
.
- Show that
can be written in the form
By expanding the integrand in powers of
 , demonstrate that
, demonstrate that
and, hence, that
Rearrange the right-hand side of the previous expression to give
(See Exercise 2.)
Thus, deduce that
- Consider the integral
where 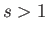 .
By expanding in powers of
.
By expanding in powers of
 , show that
, show that
where
 is a Gamma
function, and
is a Gamma
function, and
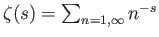 a Riemann zeta function. Likewise, demonstrate that
a Riemann zeta function. Likewise, demonstrate that
where 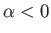 .
.
- Consider a gas consisting of identical non-interacting particles. The quantum states of
a single particle are labeled by the index
 . Let the energy of a particle in state
. Let the energy of a particle in state  be
be
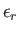 .
Let
.
Let 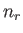 be the number of particles in quantum state
be the number of particles in quantum state  . The partition function of the gas is thus
. The partition function of the gas is thus
where the first sum is over all allowable values of the 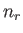 , and the second is over all single-particle
quantum states. Here,
, and the second is over all single-particle
quantum states. Here,
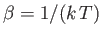 , where
, where  is the absolute temperature.
is the absolute temperature.
- Demonstrate that
- Show that
- Hence, deduce that
- Use the results of the previous exercise to show that:
- For identical, non-interacting, particles distributed according to the Maxwell-Boltzmann distribution,
- For photons,
- For identical, non-interacting, massive particles distributed according to the Bose-Einstein distribution,
Show, also, that
Hence, deduce that
- For identical, non-interacting, massive particles distributed according to the Fermi-Dirac distribution,
Show, also, that
Hence, deduce that
Note that, in the case of the Bose-Einstein distribution, the relative dispersion in 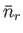 is larger than in the Maxwell-Boltzmann case, whereas
in the case of the Fermi-Dirac distribution the relative dispersion is smaller.
is larger than in the Maxwell-Boltzmann case, whereas
in the case of the Fermi-Dirac distribution the relative dispersion is smaller.
- Consider a non-relativistic free particle of mass
 in a cubical container of edge-length
in a cubical container of edge-length 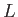 , and volume
, and volume  .
.
- Show that the energy of a general quantum state,
 , can be written
, can be written
where 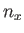 ,
, 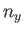 , and
, and 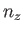 are positive integers. Hence, deduce that the contribution to the gas pressure of a particle in this state is
are positive integers. Hence, deduce that the contribution to the gas pressure of a particle in this state is
- Demonstrate that the mean pressure of a gas of weakly-interacting non-relativistic particles is
where
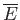 is its mean total kinetic energy, irrespective of whether the particles obey classical, Bose-Einstein, or
Fermi-Dirac statistics.
is its mean total kinetic energy, irrespective of whether the particles obey classical, Bose-Einstein, or
Fermi-Dirac statistics.
- As an electron moves in a molecule, there exists, at any instance in time, a separation of positive and negative charges within the molecule.The molecule therefore possesses a time-varying electric dipole moment,
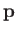 . Assuming that the molecule
is located at the origin, its instantaneous dipole moment generates an electric field
. Assuming that the molecule
is located at the origin, its instantaneous dipole moment generates an electric field
where 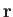 is the vector displacement from the origin.
A second molecule, located at position
is the vector displacement from the origin.
A second molecule, located at position 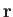 , relative to the first, develops an induced dipole moment,
, relative to the first, develops an induced dipole moment,
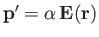 ,
in response to the electric field of the first. Here,
,
in response to the electric field of the first. Here, 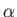 is the molecular polarizability. Moreover, the electric field
generates a force
is the molecular polarizability. Moreover, the electric field
generates a force
![$ {\bf f}'=\nabla[{\bf p}'\cdot {\bf E}({\bf r})]$](img2519.png) acting on the second molecule. (Of course, an equal and opposite
force acts on the first molecule.) Use these facts to deduce that the mean (i.e., averaged over time, and all possible orientations of
acting on the second molecule. (Of course, an equal and opposite
force acts on the first molecule.) Use these facts to deduce that the mean (i.e., averaged over time, and all possible orientations of 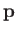 )
inter-molecular potential between a pair of neutral
molecules is attractive, and takes the form
)
inter-molecular potential between a pair of neutral
molecules is attractive, and takes the form
where
 denotes a time average.
denotes a time average.
- Consider a van der Waals gas whose equation of state is
Here, 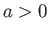 ,
, 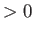 are constants, and
are constants, and  is the molar volume.
Show that the various thermodynamic potentials of the gas are:
is the molar volume.
Show that the various thermodynamic potentials of the gas are:
Here,
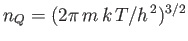 , where
, where  is the molecular mass, is known as the quantum concentration, and is the
particle concentration at which the de Broglie wavelength is equal to the mean inter-particle spacing. Obviously, the previous
expression are only valid when
is the molecular mass, is known as the quantum concentration, and is the
particle concentration at which the de Broglie wavelength is equal to the mean inter-particle spacing. Obviously, the previous
expression are only valid when
 .
.
- Show that the energy density of radiation inside a radiation-filled cavity whose walls are
held at absolute temperature
 is
is
Demonstrate that the mean pressure that the radiation exerts on the walls of the cavity is
[Hint: Modify and reuse the analysis of Exercise 7.]
- Apply the thermodynamic relation
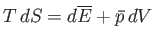 to a photon gas.
Here, we can write
to a photon gas.
Here, we can write
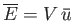 , where
, where
 is the mean energy density of
the radiation (which is independent of the volume). The radiation pressure is
is the mean energy density of
the radiation (which is independent of the volume). The radiation pressure is
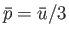 .
.
- Considering
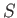 as a function of
as a function of  and
and  , show that
, show that
- Demonstrate that the mathematical identity
 leads to a differential equation for
leads to a differential equation for
 that can be integrated to give
that can be integrated to give
where 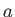 is a constant.
is a constant.
- Hence, deduce that
- Show that the total number of photons in a radiation-filled cavity of volume
 , whose walls are
held at temperature
, whose walls are
held at temperature  , is
, is
where
is a Riemann zeta function. (See Exercise 2.) Note that
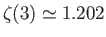 .
Demonstrate that the mean energy per photon and the entropy per photon are
.
Demonstrate that the mean energy per photon and the entropy per photon are
respectively. Note that the entropy per photon is a constant, independent of the temperature.
- Electromagnetic radiation at temperature
 fills a cavity of volume
fills a cavity of volume  . If thecavity is thermally insulated, and expands quasi-statically, show that
. If thecavity is thermally insulated, and expands quasi-statically, show that
(Neglect the heat capacity of the cavity walls.)
- The partition function for a photon gas is
where
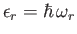 , and
, and 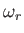 is the frequency of an individual photon state.
The spacing between the allowed frequencies can be made arbitrarily small by increasing the volume,
is the frequency of an individual photon state.
The spacing between the allowed frequencies can be made arbitrarily small by increasing the volume,  , of the
container. Hence, the sum can be approximated as an integral. Now, the number of photon states per unit volume
whose frequencies lie between
, of the
container. Hence, the sum can be approximated as an integral. Now, the number of photon states per unit volume
whose frequencies lie between  and
and
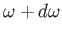 is
is
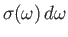 ,
where
,
where
(See Section 8.12.) Thus, we can write
Show that
Integrating by parts, demonstrate that
Hence, deduce that
[Hint: See Exercise 2.]
- Using the standard results
show that
- Show that the power per unit area radiated by a black-body of temperature
 peaks atangular frequency
peaks atangular frequency  , where
, where
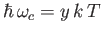 , and
, and  is the solution of the transcendental equation
is the solution of the transcendental equation
Solve this equation by iteration [i.e.,
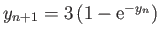 , where
, where 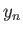 is the
is the  th guess], and, thereby,
show that
th guess], and, thereby,
show that
- A black (non-reflective) plane at temperature
 is parallel to
a black plane at temperature
is parallel to
a black plane at temperature 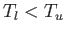 . The net energy flux density in vacuum
between the two planes is
. The net energy flux density in vacuum
between the two planes is
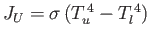 , where
, where
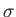 is the Stefan-Boltzmann constant. A third black plane is inserted
between the other two, and is allowed to come to a steady-state temperature
is the Stefan-Boltzmann constant. A third black plane is inserted
between the other two, and is allowed to come to a steady-state temperature
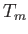 . Find
. Find 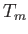 in terms of
in terms of  and
and 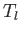 , and show that the net energy
flux is cut in half because of the presence of this plane. This is the principle
of the heat shield, and is widely used to reduce radiant heat transfer.
, and show that the net energy
flux is cut in half because of the presence of this plane. This is the principle
of the heat shield, and is widely used to reduce radiant heat transfer.
- Consider the conduction electrons in silver, which is monovalent (one free electron per atom), has a mass density
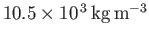 , and an atomic weight of 107. Show that the
Fermi energy (at
, and an atomic weight of 107. Show that the
Fermi energy (at  ) is
) is
and the equivalent temperature--the so-called Fermi temperature--is
Thus, if 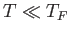 (as is definitely the case at room temperature) then the conduction electrons are highly degenerate.
Furthermore, show that at room temperature (
(as is definitely the case at room temperature) then the conduction electrons are highly degenerate.
Furthermore, show that at room temperature ( K), the contribution of the conduction electrons to the molar
specific heat is only
K), the contribution of the conduction electrons to the molar
specific heat is only
- Demonstrate that the mean pressure of the conduction electrons in a metal can be written
where 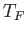 is the Fermi temperature.
(Hint: See Exercise 17.) Show that for silver (see previous exercise),
is the Fermi temperature.
(Hint: See Exercise 17.) Show that for silver (see previous exercise),
- Show that the contribution of the conduction electrons in a metal to the isothermal compressibility is
where 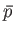 is the electron's mean pressure. Estimate
is the electron's mean pressure. Estimate 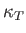 for silver. (See the previous exercise.) Compare your estimate to the
experimental value
for silver. (See the previous exercise.) Compare your estimate to the
experimental value
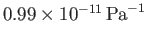 .
.
- Justify Equation (8.197).
- A system of
 bosons of mass
bosons of mass  and zero spin is in a container of volume
and zero spin is in a container of volume  , at an absolute temperature
, at an absolute temperature  . The number ofparticles is
. The number ofparticles is
[See Equation (8.227).] In the limit in which the gas is dilute,
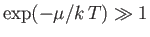 , and the Bose-Einstein distribution
becomes the Maxwell-Boltzmann distribution. Evaluate the integral in this approximation, and show that
, and the Bose-Einstein distribution
becomes the Maxwell-Boltzmann distribution. Evaluate the integral in this approximation, and show that
where
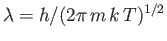 is the particles' de Broglie wavelength, and
is the particles' de Broglie wavelength, and
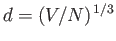 the mean inter-particle distance. Hence,
deduce that, in the classical limit, the average distance between particles is much larger than the de Broglie wavelength.
the mean inter-particle distance. Hence,
deduce that, in the classical limit, the average distance between particles is much larger than the de Broglie wavelength.



Next: Multi-Phase Systems
Up: Quantum Statistics
Previous: Bose-Einstein Condensation
Richard Fitzpatrick
2016-01-25
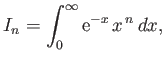
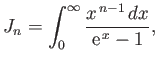
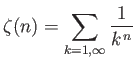
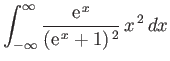
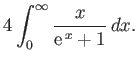
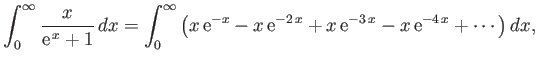
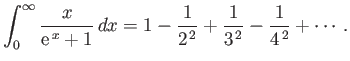
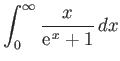
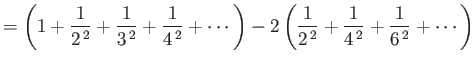
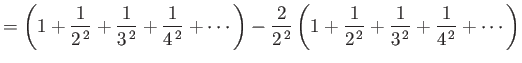
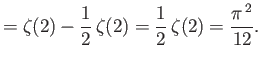
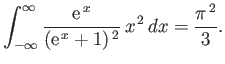
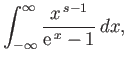
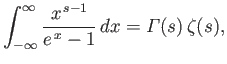


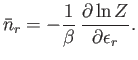
![$\displaystyle \overline{n_r^{ 2}}=\frac{1}{\beta^{ 2} Z} \frac{\partial^{ ...
...artial\ln Z}{\partial\epsilon_r}\right)+\beta^{ 2} (\bar{n}_r)^{ 2}\right].
$](img2503.png)
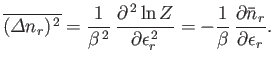

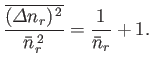
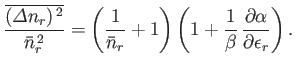
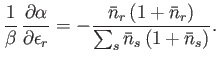
![$\displaystyle \frac{\overline{({\mit\Delta}n_r)^{ 2}}}{\bar{n}_r^{ 2}}=\left(...
...bar{n}_r)}{\sum_s \bar{n}_s (1+\bar{n}_s)}\right]\simeq\frac{1}{\bar{n}_r}+1.
$](img2509.png)
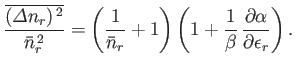
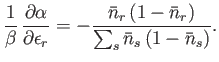
![$\displaystyle \frac{\overline{({\mit\Delta}n_r)^{ 2}}}{\bar{n}_r^{ 2}}=\left(...
...bar{n}_r)}{\sum_s \bar{n}_s (1-\bar{n}_s)}\right]\simeq\frac{1}{\bar{n}_r}-1.
$](img2511.png)
 , can be written
, can be written
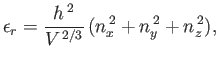
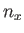 ,
, 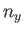 , and
, and 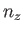 are positive integers. Hence, deduce that the contribution to the gas pressure of a particle in this state is
are positive integers. Hence, deduce that the contribution to the gas pressure of a particle in this state is
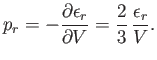

 is its mean total kinetic energy, irrespective of whether the particles obey classical, Bose-Einstein, or
Fermi-Dirac statistics.
is its mean total kinetic energy, irrespective of whether the particles obey classical, Bose-Einstein, or
Fermi-Dirac statistics.

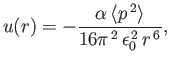
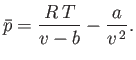
![$\displaystyle =-\nu R T\left\{\ln\left[\frac{n_Q}{N_A} (v-b)\right]+1\right\}-\frac{\nu a}{v},$](img2526.png)
![$\displaystyle =\nu R\left\{\ln\left[\frac{n_Q}{N_A} (v-b)\right]+\frac{5}{2}\right\},$](img2527.png)
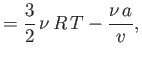

![$\displaystyle =\nu R T\left\{-\ln\left[\frac{n_Q}{N_A} (v-b)\right]+\frac{v}{v-b}-1\right\}-\frac{2 \nu a}{v}.$](img2532.png)

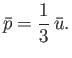
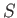 as a function of
as a function of  and
and  , show that
, show that
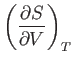
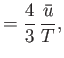

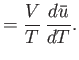
 leads to a differential equation for
leads to a differential equation for
 that can be integrated to give
that can be integrated to give
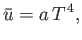
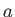 is a constant.
is a constant.

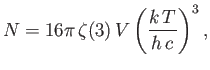
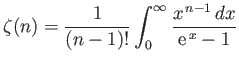
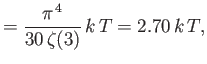
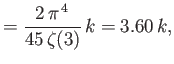
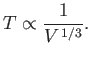
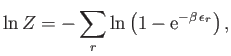
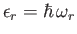 , and
, and 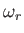 is the frequency of an individual photon state.
The spacing between the allowed frequencies can be made arbitrarily small by increasing the volume,
is the frequency of an individual photon state.
The spacing between the allowed frequencies can be made arbitrarily small by increasing the volume,  , of the
container. Hence, the sum can be approximated as an integral. Now, the number of photon states per unit volume
whose frequencies lie between
, of the
container. Hence, the sum can be approximated as an integral. Now, the number of photon states per unit volume
whose frequencies lie between  and
and
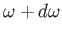 is
is
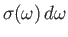 ,
where
,
where
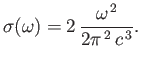
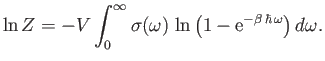
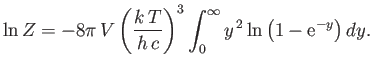


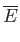

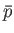
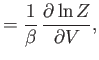
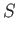
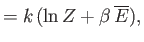
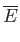
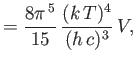
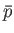

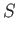
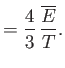
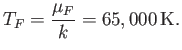
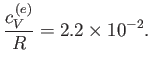
![$\displaystyle \bar{p} = \frac{2}{5} \frac{N k T_F}{V}\left[1+\frac{5\pi^{ 2}}{12}\left(\frac{T}{T_F}\right)^{ 2} + \cdots\right],
$](img2586.png)