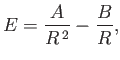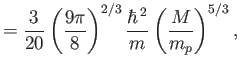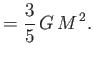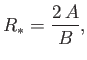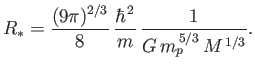Next: Chandrasekhar Limit
Up: Quantum Statistics
Previous: Sommerfeld Expansion
A main-sequence hydrogen-burning star, such as the Sun, is maintained
in equilibrium via the balance of the gravitational attraction tending
to make it collapse, and the thermal pressure tending to make it expand.
Of course, the
thermal energy of the star is generated by nuclear reactions occurring deep inside
its core. Eventually, however, the star will run out of burnable fuel, and will, therefore,
start to collapse, as it radiates away its remaining thermal energy.
What is the ultimate fate of such a star?
A burnt-out star is basically a gas of electrons and ions. As the
star collapses, its density increases, so the mean separation between its
constituent particles decreases. Eventually, the mean separation becomes
of order the de Broglie wavelength of the electrons, and the electron
gas becomes degenerate. Note, that the de Broglie wavelength of the
ions is much smaller than that of the electrons (because of the ions' much larger mass), so the ion gas remains
non-degenerate. Now, even at
zero temperature, a degenerate electron gas exerts a substantial pressure,
because the Pauli exclusion principle prevents the mean electron separation
from becoming significantly smaller than the typical
de Broglie wavelength. (See Section 8.15 and Exercise 18.) Thus, it is possible for a burnt-out star to maintain
itself against complete collapse under gravity via the degeneracy pressure
of its constituent electrons. Such stars are termed white-dwarfs.
Let us investigate the physics of white-dwarfs in more detail.
The total energy of a white-dwarf star can be written
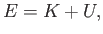 |
(8.192) |
where 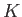 is the total kinetic energy of the degenerate electrons (the kinetic
energy of the ions is negligible), and
is the total kinetic energy of the degenerate electrons (the kinetic
energy of the ions is negligible), and 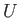 is the gravitational potential
energy. Let us assume, for the sake of simplicity, that the density of the
star is uniform. In this case, the gravitational potential
energy takes the form
is the gravitational potential
energy. Let us assume, for the sake of simplicity, that the density of the
star is uniform. In this case, the gravitational potential
energy takes the form
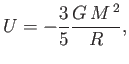 |
(8.193) |
where 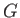 is the gravitational constant,
is the gravitational constant, 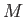 the stellar mass, and
the stellar mass, and 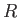 the stellar radius.
the stellar radius.
Let us assume that the electron gas is highly degenerate, which is
equivalent to taking the limit
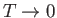 . In this case, we know,
from Section 8.15, that the Fermi momentum can be written
. In this case, we know,
from Section 8.15, that the Fermi momentum can be written
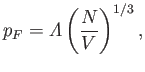 |
(8.194) |
where
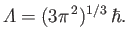 |
(8.195) |
Here,
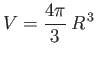 |
(8.196) |
is the stellar volume, and  the total number of electrons contained
in the star. Furthermore, the number of
electron states contained in an annular radius of
the total number of electrons contained
in the star. Furthermore, the number of
electron states contained in an annular radius of 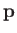 -space
lying between radii
-space
lying between radii 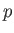 and
and 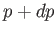 is
is
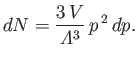 |
(8.197) |
(See Exercise 20.)
Hence, the total kinetic energy of the electron gas can be written
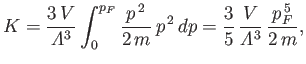 |
(8.198) |
where 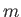 is the electron mass. It follows that
is the electron mass. It follows that
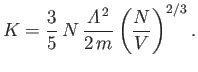 |
(8.199) |
The interior of a white-dwarf star is composed of atoms like
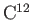 and
and
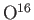 that contain equal numbers of protons, neutrons, and
electrons. Thus,
that contain equal numbers of protons, neutrons, and
electrons. Thus,
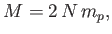 |
(8.200) |
where 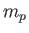 is the proton mass.
is the proton mass.
Equations (8.192), (8.193), (8.195), (8.196),
(8.199), and (8.200) can be combined to give
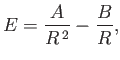 |
(8.201) |
where
The equilibrium radius of the star, 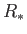 , is that which
minimizes the total energy,
, is that which
minimizes the total energy,  . In fact,
it is easily demonstrated that
. In fact,
it is easily demonstrated that
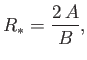 |
(8.204) |
which yields
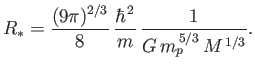 |
(8.205) |
The previous formula can also be written
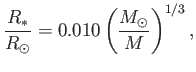 |
(8.206) |
where
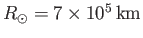 is the solar radius, and
is the solar radius, and
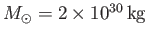 the solar mass. It follows that
the radius of a typical solar-mass white-dwarf is about 7000km:
that is, about the same as the radius of the Earth. The first
white-dwarf to be discovered (in 1862) was the companion of Sirius. Nowadays,
thousands of white-dwarfs have been observed, all with properties similar
to those described previously.
the solar mass. It follows that
the radius of a typical solar-mass white-dwarf is about 7000km:
that is, about the same as the radius of the Earth. The first
white-dwarf to be discovered (in 1862) was the companion of Sirius. Nowadays,
thousands of white-dwarfs have been observed, all with properties similar
to those described previously.



Next: Chandrasekhar Limit
Up: Quantum Statistics
Previous: Sommerfeld Expansion
Richard Fitzpatrick
2016-01-25
![]() . In this case, we know,
from Section 8.15, that the Fermi momentum can be written
. In this case, we know,
from Section 8.15, that the Fermi momentum can be written
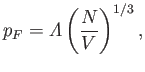
![]() and
and
![]() that contain equal numbers of protons, neutrons, and
electrons. Thus,
that contain equal numbers of protons, neutrons, and
electrons. Thus,