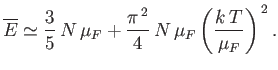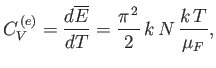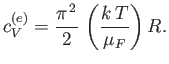Next: White-Dwarf Stars
Up: Quantum Statistics
Previous: Conduction Electrons in Metal
Let us examine the conduction electrons in a metal in slightly more detail. In particular, let us try to obtain a more exact
expression for the electronic specific heat. We saw in the previous section that the
Fermi energy,  , is determined by the equation
, is determined by the equation
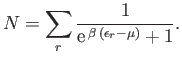 |
(8.154) |
Likewise, the mean electron energy is
 |
(8.155) |
Because, in general, the energies of the quantum states are very closely spaced, the sums in the previous two expressions can
be replaced by integrals. Now, according to Section 8.12, the number of quantum states per unit volume
with wavenumbers in the range  to
to 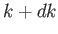 is
is
 |
(8.156) |
However, the energy of a state with wavenumber  is
is
 |
(8.157) |
where  is the electron mass. Let
is the electron mass. Let
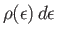 be the number of electrons
whose energies lies in the range
be the number of electrons
whose energies lies in the range 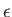 to
to
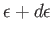 . It follows that
. It follows that
 |
(8.158) |
where the factor of 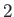 is to take into account the two possible spin states which exist for each translational state.
Hence,
is to take into account the two possible spin states which exist for each translational state.
Hence,
 |
(8.159) |
Moreover, Equations (8.154) and (8.155) become
where
 |
(8.162) |
is the Fermi function.
The integrals on the right-hand sides of Equations (8.160) and (8.161) are both of the general form
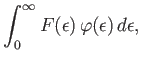 |
(8.163) |
where
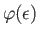 is a smoothly varying function of
is a smoothly varying function of 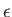 . Let
. Let
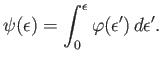 |
(8.164) |
We can integrate Equation (8.163) by parts to give
![$\displaystyle \int_0^\infty F(\epsilon) \varphi(\epsilon) d\epsilon = \left[F...
...psilon)\right]_0^\infty -\int_0^\infty F'(\epsilon) \psi(\epsilon) d\epsilon,$](img2310.png) |
(8.165) |
which reduces to
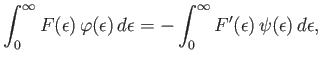 |
(8.166) |
because
 . Here,
. Here,
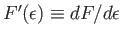 .
.
Now, if
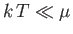 then
then
 is a constant everywhere, apart from a thin region of thickness
is a constant everywhere, apart from a thin region of thickness 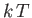 , centered on
, centered on
 . (See Figure 8.4.)
It follows that
. (See Figure 8.4.)
It follows that
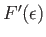 is approximately zero everywhere, apart from in this region. Hence, the relatively slowly-varying
function
is approximately zero everywhere, apart from in this region. Hence, the relatively slowly-varying
function
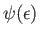 can be Taylor expanded about
can be Taylor expanded about
 :
:
![$\displaystyle \psi(\epsilon) = \sum_{m=0,\infty}\frac{1}{m!}\left[\frac{d^{ m}\psi}{d\epsilon^{ m}}\right]_\mu (\epsilon-\mu)^m.$](img2317.png) |
(8.167) |
Thus, Equation (8.166) becomes
![$\displaystyle \int_0^\infty F(\epsilon) \varphi(\epsilon) d\epsilon =-\sum_{m...
...silon^{ m}}\right]_\mu\int_0^\infty F'(\epsilon) (\epsilon-\mu)^m d\epsilon.$](img2318.png) |
(8.168) |
From Equation (8.162), we have
![$\displaystyle \int_0^\infty F'(\epsilon) (\epsilon-\mu)^m d\epsilon=-\int_0^\...
...u)}}{[{\rm e}^{ \beta (\epsilon-\mu)}+1]^{ 2}} (\epsilon-\mu)^m d\epsilon,$](img2319.png) |
(8.169) |
which becomes
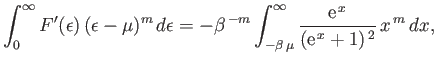 |
(8.170) |
where
 . However, because the integrand has a sharp maximum at
. However, because the integrand has a sharp maximum at  , and because
, and because
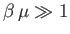 , we can
replace the lower limit of integration by
, we can
replace the lower limit of integration by  with negligible error. Thus, we obtain
with negligible error. Thus, we obtain
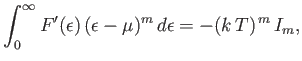 |
(8.171) |
where
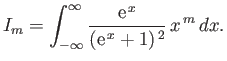 |
(8.172) |
Note that
 |
(8.173) |
is an even function of  . It follows, by symmetry, that
. It follows, by symmetry, that 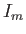 is zero when
is zero when  is odd.
Moreover,
is odd.
Moreover,
![$\displaystyle I_0 = \int_{-\infty}^\infty \frac{{\rm e}^{ x}}{({\rm e}^{ x}+1)^{ 2}} dx= -\left[\frac{1}{{\rm e}^{ x}+1}\right]_{-\infty}^{\infty} = 1.$](img2329.png) |
(8.174) |
Finally, it can be demonstrated that
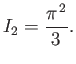 |
(8.175) |
(See Exercise 3.)
Hence, we deduce that
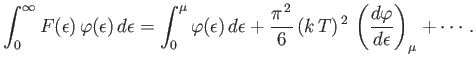 |
(8.176) |
This expansion is known as the Sommerfeld expansion, after its inventor, Arnold Sommerfeld.
Equation (8.160) yields
 |
(8.177) |
However, it follows from Equation (8.159) that
Hence,
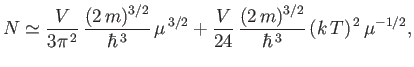 |
(8.180) |
which can also be written
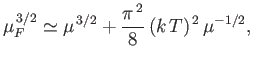 |
(8.181) |
where 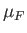 is the Fermi energy at
is the Fermi energy at  . [See Equation (8.144).] The previous equation can
be rearranged to give
. [See Equation (8.144).] The previous equation can
be rearranged to give
![$\displaystyle \mu\simeq \mu_F\left[1+\frac{\pi^{ 2}}{8}\left(\frac{k T}{\mu}\right)^2\right]^{-2/3},$](img2339.png) |
(8.182) |
which reduces to
![$\displaystyle \mu\simeq \mu_F\left[1-\frac{\pi^{ 2}}{12}\left(\frac{k T}{\mu_F}\right)^2\right],$](img2340.png) |
(8.183) |
assuming that
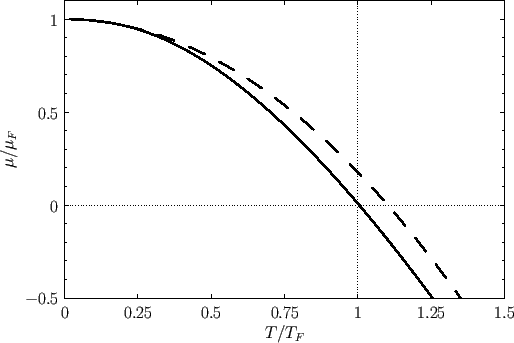
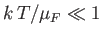 . Figure 8.6 shows a comparison between the previous approximate expression for the temperature variation of the Fermi
energy of a degenerate electron gas and the numerically-calculated exact value. It can be seen that our approximate expression is surprisingly accurate (at least,
for
. Figure 8.6 shows a comparison between the previous approximate expression for the temperature variation of the Fermi
energy of a degenerate electron gas and the numerically-calculated exact value. It can be seen that our approximate expression is surprisingly accurate (at least,
for
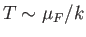 ).
).
Figure:
The solid curve shows the numerically-calculated exact Fermi energy of a degenerate electron gas as a function of the temperature.
The dashed curve shows the analytic approximation
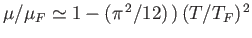 . Here,
. Here,
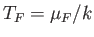 is known as the Fermi temperature.
is known as the Fermi temperature.
 |
Equation (8.161) yields
![$\displaystyle \overline{E} = \int_0^\mu \epsilon \rho(\epsilon) d\epsilon + \...
...{6} (k T)^{ 2}\left[\frac{d(\epsilon \rho)}{d\epsilon}\right]_\mu + \cdots.$](img2345.png) |
(8.184) |
However, it follows from Equation (8.159) that
Hence,
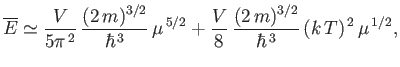 |
(8.187) |
which can also be written
![$\displaystyle \overline{E} \simeq \frac{3}{5} N \mu_F\left[\left(\frac{\mu}{\...
...4}\left(\frac{k T}{\mu_F}\right)^2\left(\frac{\mu}{\mu_F}\right)^{1/2}\right].$](img2351.png) |
(8.188) |
Making use of Equation (8.183), and only retaining terms up to second order in
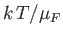 , we obtain
, we obtain
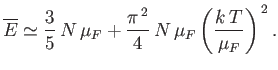 |
(8.189) |
Hence, the specific heat capacity of the conduction electrons becomes
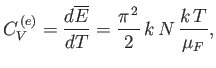 |
(8.190) |
and the molar specific heat is written
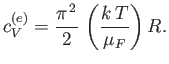 |
(8.191) |
Of course, because
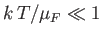 , this value is much less than the classical estimate,
, this value is much less than the classical estimate, 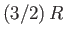 .
.



Next: White-Dwarf Stars
Up: Quantum Statistics
Previous: Conduction Electrons in Metal
Richard Fitzpatrick
2016-01-25
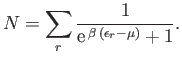



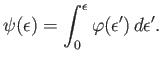
![$\displaystyle \int_0^\infty F(\epsilon) \varphi(\epsilon) d\epsilon = \left[F...
...psilon)\right]_0^\infty -\int_0^\infty F'(\epsilon) \psi(\epsilon) d\epsilon,$](img2310.png)
![]() then
then
![]() is a constant everywhere, apart from a thin region of thickness
is a constant everywhere, apart from a thin region of thickness ![]() , centered on
, centered on
![]() . (See Figure 8.4.)
It follows that
. (See Figure 8.4.)
It follows that
![]() is approximately zero everywhere, apart from in this region. Hence, the relatively slowly-varying
function
is approximately zero everywhere, apart from in this region. Hence, the relatively slowly-varying
function
![]() can be Taylor expanded about
can be Taylor expanded about
![]() :
:
![$\displaystyle \psi(\epsilon) = \sum_{m=0,\infty}\frac{1}{m!}\left[\frac{d^{ m}\psi}{d\epsilon^{ m}}\right]_\mu (\epsilon-\mu)^m.$](img2317.png)
![$\displaystyle \int_0^\infty F(\epsilon) \varphi(\epsilon) d\epsilon =-\sum_{m...
...silon^{ m}}\right]_\mu\int_0^\infty F'(\epsilon) (\epsilon-\mu)^m d\epsilon.$](img2318.png)
![$\displaystyle \int_0^\infty F'(\epsilon) (\epsilon-\mu)^m d\epsilon=-\int_0^\...
...u)}}{[{\rm e}^{ \beta (\epsilon-\mu)}+1]^{ 2}} (\epsilon-\mu)^m d\epsilon,$](img2319.png)
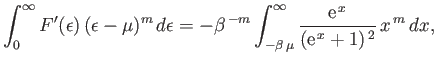
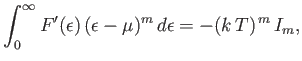
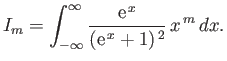

![$\displaystyle I_0 = \int_{-\infty}^\infty \frac{{\rm e}^{ x}}{({\rm e}^{ x}+1)^{ 2}} dx= -\left[\frac{1}{{\rm e}^{ x}+1}\right]_{-\infty}^{\infty} = 1.$](img2329.png)
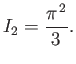
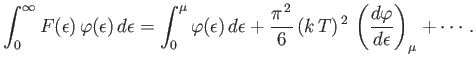


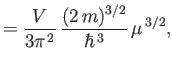
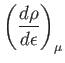
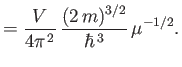
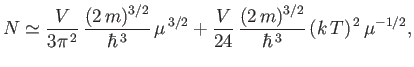
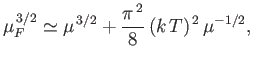
![$\displaystyle \mu\simeq \mu_F\left[1+\frac{\pi^{ 2}}{8}\left(\frac{k T}{\mu}\right)^2\right]^{-2/3},$](img2339.png)

![$\displaystyle \overline{E} = \int_0^\mu \epsilon \rho(\epsilon) d\epsilon + \...
...{6} (k T)^{ 2}\left[\frac{d(\epsilon \rho)}{d\epsilon}\right]_\mu + \cdots.$](img2345.png)
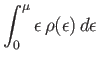

![$\displaystyle \left[\frac{d(\epsilon \rho)}{d\epsilon}\right]_\mu$](img2348.png)
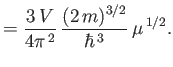
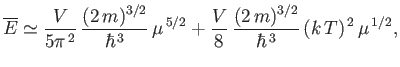
![$\displaystyle \overline{E} \simeq \frac{3}{5} N \mu_F\left[\left(\frac{\mu}{\...
...4}\left(\frac{k T}{\mu_F}\right)^2\left(\frac{\mu}{\mu_F}\right)^{1/2}\right].$](img2351.png)