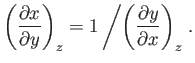
This result is known as the reciprocal rule of partial differentiation.
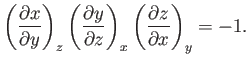
This result is also known as the cyclic rule of partial differentiation. Hence, deduce that

- What is the increase in temperature of the water?
- How far from the left end of the cylinder will the piston come to rest?
- What is the increase in total entropy of the system?
- Does the temperature of the gas increase, decrease, or remain the same?
- Does the entropy of the gas increase, decrease, or remain the same?
- Show that the final temperature of the gas is
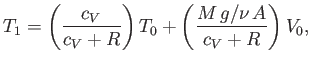
where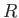 is the molar ideal gas constant.
is the molar ideal gas constant.
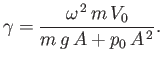
By analyzing one-dimensional compressions and rarefactions of the system of fluid
contained in a slab of thickness ![]() , show that the pressure,
, show that the pressure, ![]() , in the
fluid depends on the position,
, in the
fluid depends on the position, ![]() , and the time,
, and the time, ![]() , so as to satisfy the
wave equation
, so as to satisfy the
wave equation
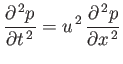
where the velocity of sound propagation,
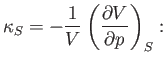
that is, its compressibility measured under conditions in which the fluid is thermally insulated.
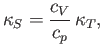
where
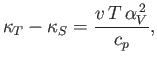
where
- Show that adiabatic compressibility,
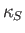 , of an ideal gas is
, of an ideal gas is

where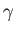 is the ratio of specific heats, and
is the ratio of specific heats, and  the gas pressure.
the gas pressure.
- Show that the velocity of sound in an ideal gas
is
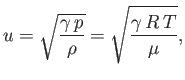
where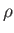 is the mass density,
is the mass density, 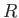 the molar ideal gas constant,
the molar ideal gas constant,  the absolute temperature, and
the absolute temperature, and  the molecular weight.
the molecular weight.
- How does the sound velocity depend on the gas temperature,
 , at a fixed
pressure? How does it depend on the gas pressure,
, at a fixed
pressure? How does it depend on the gas pressure,  , at fixed temperature?
, at fixed temperature?
- Calculate the velocity of sound in nitrogen
(
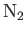 ) gas at room temperature
and pressure (i.e.,
) gas at room temperature
and pressure (i.e., 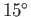 C at 1 bar). Take
C at 1 bar). Take
 .
.

where
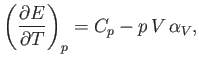
and
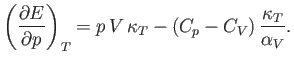
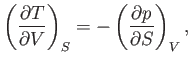
derive the other three by making use of the reciprocal and cyclic rules of partial differentiation (see Exercises 1 and 2), as well as the identity
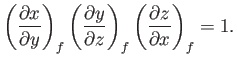
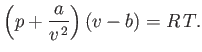
The critical point is defined as the unique point at which
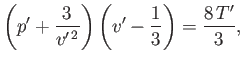
where
-
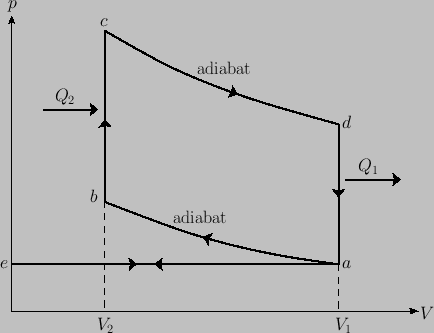
 : Isobaric (i.e., constant pressure) intake (at atmospheric pressure).
: Isobaric (i.e., constant pressure) intake (at atmospheric pressure).
-
 : Adiabatic compression (compression stroke).
: Adiabatic compression (compression stroke).
-
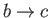 : Isochoric (i.e., constant volume) increase of temperature during ignition. (Gas combustion is
an irreversible process. Here, it is replaced by a reversible isochoric process in which heat is assumed to flow into
the system from a reservoir.)
: Isochoric (i.e., constant volume) increase of temperature during ignition. (Gas combustion is
an irreversible process. Here, it is replaced by a reversible isochoric process in which heat is assumed to flow into
the system from a reservoir.)
-
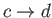 : Adiabatic expansion (power stroke).
: Adiabatic expansion (power stroke).
-
 : Isochoric decrease of temperature (exhaust value opened).
: Isochoric decrease of temperature (exhaust value opened).
-
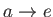 : Isobaric exhaust (at atmospheric pressure).
: Isobaric exhaust (at atmospheric pressure).
- Assume that the working substance is an ideal gas. Show that the efficiency of the cycle is
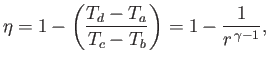
where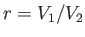 is the compression ratio of the engine.
is the compression ratio of the engine.
- Calculate
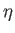 for the realistic values
for the realistic values  and
and
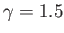 .
.