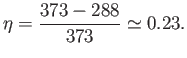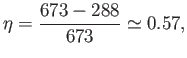Next: Refrigerators
Up: Classical Thermodynamics
Previous: Joule-Thompson Throttling
Thermodynamics was invented, almost by accident, in 1825, by a young French engineer
called Sadi Carnot, who was investigating the theoretical
limitations on the efficiency of
steam engines.
Although, nowadays, we are not particularly interested in steam engines, it is
still highly instructive to review some of Carnot's arguments.
We know, by observation, that it is possible to do mechanical work 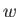 upon a device
upon a device 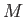 , and then to extract an equivalent amount of heat
, and then to extract an equivalent amount of heat 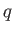 , which
goes to increase the internal energy of some heat reservoir. (Here, we use the small
letters
, which
goes to increase the internal energy of some heat reservoir. (Here, we use the small
letters 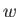 and
and 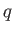 to denote intrinsically positive amounts of work and
heat, respectively.)
An good example of this process is Joule's classic experiment by which he verified
the first law of thermodynamics. A paddle wheel is spun in a liquid by a falling
weight, and the work done by the weight on the wheel
is converted into heat, and absorbed by the liquid. Carnot's question was
the following. Is it
possible to reverse this process, and build a device, called a heat engine, that
extracts heat energy from a reservoir, and converts it into useful macroscopic work?
For instance, is it possible to extract heat from the ocean, and use it to run
an electric generator?
to denote intrinsically positive amounts of work and
heat, respectively.)
An good example of this process is Joule's classic experiment by which he verified
the first law of thermodynamics. A paddle wheel is spun in a liquid by a falling
weight, and the work done by the weight on the wheel
is converted into heat, and absorbed by the liquid. Carnot's question was
the following. Is it
possible to reverse this process, and build a device, called a heat engine, that
extracts heat energy from a reservoir, and converts it into useful macroscopic work?
For instance, is it possible to extract heat from the ocean, and use it to run
an electric generator?
There are a few caveats to Carnot's question. First of all,
the work should not be done
at the expense of the heat engine itself, otherwise the conversion of heat into
work could not continue indefinitely. We can ensure that this is the
case by demanding that the heat engine perform some sort of cycle,
by which it periodically returns to the same macrostate, but, in the meantime, has
extracted heat from the reservoir, and done an equivalent amount of useful work.
A cyclic process seems reasonable, because we know that both
steam engines and internal
combustion
engines perform continuous cycles. The second caveat is that the work done by
the heat engine should be such as to change a single parameter of
some external device (e.g., by lifting a weight), without doing it at the
expense of affecting the other degrees of freedom, or the entropy, of that device.
For instance, if we are extracting heat from the ocean to
generate electricity, we want to spin the shaft
of the electrical generator without increasing the generator's
entropy--that is, without causing the generator
to heat up, or fall to bits.
Let us examine the feasibility of a heat engine using the laws of
thermodynamics. Suppose that a heat engine, 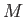 , performs a single cycle. Because
, performs a single cycle. Because
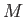 has returned to its initial macrostate, its internal energy is
unchanged, and the first law of thermodynamics tell us that the work done
by the engine,
has returned to its initial macrostate, its internal energy is
unchanged, and the first law of thermodynamics tell us that the work done
by the engine, 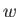 , must equal the heat extracted from the reservoir,
, must equal the heat extracted from the reservoir, 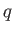 , so that
, so that
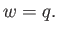 |
(6.191) |
The previous condition is certainly a necessary
condition for a feasible heat engine.
But, is it also a sufficient condition? In other words, does
every device that
satisfies this condition actually work? Let us think a little more carefully
about what we are actually expecting a heat engine to do. We want to construct a
device that will extract energy from a heat reservoir, where it is randomly
distributed over very many degrees of freedom, and convert it into energy
distributed over a single degree of freedom associated
with some parameter of an external
device. Once we have expressed the problem in these terms, it is fairly obvious that
what
we are really asking for is a spontaneous transition from a probable to an improbable
state, which we know is forbidden by the second law of thermodynamics. So,
unfortunately, we cannot run an electric generator off heat extracted from the
ocean, because this is equivalent to expecting all of the molecules in the ocean, which are moving in random directions, to all suddenly all move in the same direction, so as to
exert a force on some lever, say, that can then be converted into a torque on the
generator shaft. We know, from our investigation of statistical thermodynamics, that such a process--although, in principle,
possible--is fantastically improbable.
The improbability of the scenario just outlined is summed up in the second law
of thermodynamics, which says that the total entropy of an isolated system
can never spontaneously decrease, so
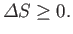 |
(6.192) |
For the case of a heat engine, the isolated system consists of the engine, the
reservoir from which it extracts heat, and the outside device upon which it
does work. The engine itself returns periodically
to the same state, so its
entropy is clearly unchanged after each cycle. We have already specified that there
is no change in the entropy of the external device upon which the work is done. On
the other hand, the entropy change per cycle of the heat reservoir,
which is held at absolute temperature
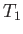 , say, is given by
, say, is given by
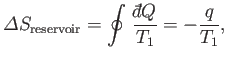 |
(6.193) |
where
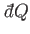 is the infinitesimal heat absorbed by the reservoir, and the integral
is taken over a whole cycle of the heat engine. The integral can be converted into
the expression
is the infinitesimal heat absorbed by the reservoir, and the integral
is taken over a whole cycle of the heat engine. The integral can be converted into
the expression 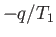 because the amount of heat extracted by the engine is
assumed to be too small to modify the temperature of the reservoir (which is
the definition of a heat reservoir), so that
because the amount of heat extracted by the engine is
assumed to be too small to modify the temperature of the reservoir (which is
the definition of a heat reservoir), so that 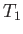 is a constant during the cycle.
The second law of thermodynamics reduces to
is a constant during the cycle.
The second law of thermodynamics reduces to
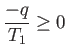 |
(6.194) |
or, making use of the first law of thermodynamics,
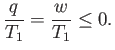 |
(6.195) |
Because we wish the work, 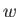 , done by the engine to be positive, the previous relation
clearly
cannot be satisfied, which proves that an engine that converts heat
directly into work is thermodynamically impossible.
, done by the engine to be positive, the previous relation
clearly
cannot be satisfied, which proves that an engine that converts heat
directly into work is thermodynamically impossible.
A perpetual motion device,
which continuously executes a cycle without extracting heat from,
or doing work on, its surroundings,
is possible according to Equation (6.195). In fact, such a device
corresponds to the equality sign in Equation (6.192), which
implies that the device must be completely
reversible. In reality, there is no such thing as a completely reversible engine.
All engines, even the most efficient, have frictional losses that render them,
at least,
slightly irreversible. Thus, the equality sign in Equation (6.192) corresponds to
an asymptotic limit that reality can closely approach, but never quite attain.
It follows that a perpetual motion device is thermodynamically impossible.
Nevertheless, the US patent office receives about 100 patent
applications a year regarding perpetual motion devices. The British patent office,
being slightly less open-minded that its American counterpart, refuses to entertain
such applications on the basis that perpetual motion devices are forbidden by
the second law of thermodynamics.
According to Equation (6.195), there is no thermodynamic objection to
a heat engine that runs backwards, and converts work directly into heat. This
is not surprising, because we know that this is essentially what frictional forces
do. Clearly, we have, here, another example of a natural process that is
fundamentally irreversible according to the second law of thermodynamics.
In fact, the statement
It is impossible to construct a perfect heat engine that converts
heat directly into work
is called Kelvin's formulation of the second law.
We have demonstrated that a perfect heat engine, that converts
heat directly into work, is impossible. But, there must be some way of
obtaining useful work from heat energy, otherwise steam engines would not operate.
The reason that our
previous scheme did not work was that it decreased the entropy of a heat reservoir,
held at some temperature 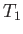 ,
by extracting an amount of heat
,
by extracting an amount of heat 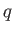 per cycle,
without any compensating increase in the entropy of anything else, so the
second law of thermodynamics was violated. How can we remedy this situation?
We still want
the heat engine itself to perform periodic cycles (so,
by definition, its entropy cannot increase over a
cycle), and we also do not
want to increase the entropy of the external device upon which the
work is done. Our only other option is to increase the entropy of some other
body. In Carnot's analysis, this other body is
a second heat reservoir held at temperature
per cycle,
without any compensating increase in the entropy of anything else, so the
second law of thermodynamics was violated. How can we remedy this situation?
We still want
the heat engine itself to perform periodic cycles (so,
by definition, its entropy cannot increase over a
cycle), and we also do not
want to increase the entropy of the external device upon which the
work is done. Our only other option is to increase the entropy of some other
body. In Carnot's analysis, this other body is
a second heat reservoir held at temperature 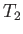 . We can increase the entropy
of the second reservoir by dumping some of the heat that we extracted from the
first reservoir into it. Suppose that the heat per cycle that we extract from the first
reservoir
is
. We can increase the entropy
of the second reservoir by dumping some of the heat that we extracted from the
first reservoir into it. Suppose that the heat per cycle that we extract from the first
reservoir
is 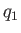 , and the heat per cycle that we reject into the second reservoir
is
, and the heat per cycle that we reject into the second reservoir
is 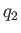 . Let the
work done on the external device be
. Let the
work done on the external device be 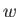 per cycle. The first law of thermodynamics
implies that
per cycle. The first law of thermodynamics
implies that
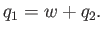 |
(6.196) |
Note that if 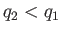 then positive (i.e., useful) work is done on the
external device.
The total entropy change per cycle is a consequence of the heat extracted from the first
reservoir, and the heat dumped into the second, and must be positive (or zero),
according to the second law of thermodynamics. So,
then positive (i.e., useful) work is done on the
external device.
The total entropy change per cycle is a consequence of the heat extracted from the first
reservoir, and the heat dumped into the second, and must be positive (or zero),
according to the second law of thermodynamics. So,
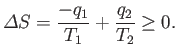 |
(6.197) |
We can combine the previous two equations to give
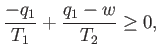 |
(6.198) |
or
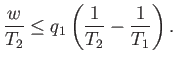 |
(6.199) |
It is clear that the engine is only going to perform useful work (i.e., 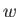 is
only going to be positive) if
is
only going to be positive) if 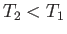 . So, the second reservoir must be colder than
the first if the heat dumped into the former is to increase the
entropy of the universe more than
the heat extracted from the latter decreases it. It is useful to define the
efficiency,
. So, the second reservoir must be colder than
the first if the heat dumped into the former is to increase the
entropy of the universe more than
the heat extracted from the latter decreases it. It is useful to define the
efficiency, 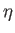 , of a heat engine. This is the ratio of the work done per cycle
on the external device to
the heat energy absorbed per cycle from the first reservoir. The efficiency of a
perfect heat engine is unity, but we have already shown that such an engine
is impossible. What is the efficiency of a realizable engine? It is clear,
from the previous equation, that
, of a heat engine. This is the ratio of the work done per cycle
on the external device to
the heat energy absorbed per cycle from the first reservoir. The efficiency of a
perfect heat engine is unity, but we have already shown that such an engine
is impossible. What is the efficiency of a realizable engine? It is clear,
from the previous equation, that
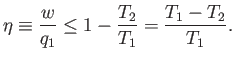 |
(6.200) |
Note that the efficiency is always less than unity. A real engine must always
reject some energy into the second heat reservoir, in order to satisfy the second
law of thermodynamics, so less energy is available to do external
work, and the efficiency
of the engine is reduced. The equality sign in the previous expression corresponds
to a completely reversible heat engine (i.e., one that is quasi-static). It
is
clear that real engines, which are always irreversible to some extent, are
less efficient than reversible engines. Furthermore, all reversible engines
that operate between the two temperatures 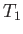 and
and 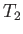 have the
same efficiency,
have the
same efficiency,
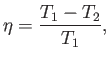 |
(6.201) |
irrespective of the manner in which they operate.
Let us consider how we might construct a reversible heat engine.
Suppose that we have some gas in a cylinder equipped with a frictionless piston.
The gas is not necessarily a perfect gas. Suppose that we also have two heat
reservoirs held at temperatures 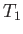 and
and 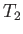 (where
(where 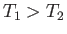 ). These
reservoirs might take the form of large water baths.
Let us start off with the
gas in thermal contact with the first reservoir. We now pull the piston out,
very slowly, so that heat energy flows reversibly into the gas from the
reservoir. Let us now thermally isolate the gas, and slowly pull out
the piston some more. During this adiabatic process, the temperature of the
gas falls (because there is no longer any heat flowing into it to
compensate for the work it does on the piston). Let us continue this process
until the temperature of the gas falls to
). These
reservoirs might take the form of large water baths.
Let us start off with the
gas in thermal contact with the first reservoir. We now pull the piston out,
very slowly, so that heat energy flows reversibly into the gas from the
reservoir. Let us now thermally isolate the gas, and slowly pull out
the piston some more. During this adiabatic process, the temperature of the
gas falls (because there is no longer any heat flowing into it to
compensate for the work it does on the piston). Let us continue this process
until the temperature of the gas falls to 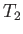 . We now place the
gas in thermal contact with the second reservoir, and slowly push the piston
in. During this isothermal
process, heat flows out of the gas into the reservoir. We next
thermally isolate the gas a second time, and slowly compress it some more. In this
process, the temperature of the gas increases. We stop the compression when the temperature
reaches
. We now place the
gas in thermal contact with the second reservoir, and slowly push the piston
in. During this isothermal
process, heat flows out of the gas into the reservoir. We next
thermally isolate the gas a second time, and slowly compress it some more. In this
process, the temperature of the gas increases. We stop the compression when the temperature
reaches 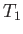 . If we carry out each step properly then we can return the gas to
its initial state, and then repeat the cycle ad infinitum.
We now have a set of reversible processes by which a quantity
of heat is extracted from the
first reservoir, and a quantity of heat is dumped into the second. We can best
evaluate
the work done by the system during each cycle
by plotting out the locus of the gas in a
. If we carry out each step properly then we can return the gas to
its initial state, and then repeat the cycle ad infinitum.
We now have a set of reversible processes by which a quantity
of heat is extracted from the
first reservoir, and a quantity of heat is dumped into the second. We can best
evaluate
the work done by the system during each cycle
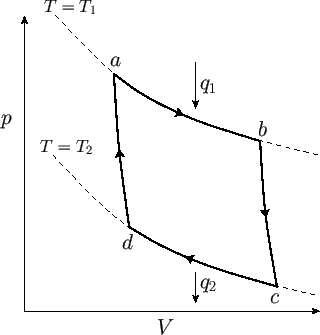
by plotting out the locus of the gas in a 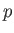 -
- diagram. The locus takes the form of a closed curve. See Figure 6.3.
The net work done per cycle is the ``area'' enclosed within this curve, because
diagram. The locus takes the form of a closed curve. See Figure 6.3.
The net work done per cycle is the ``area'' enclosed within this curve, because
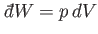 [if
[if 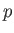 is plotted vertically, and
is plotted vertically, and  horizontally,
then
horizontally,
then 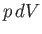 is clearly an element of area under the curve
is clearly an element of area under the curve 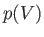 ].
The engine we have
just described is called a Carnot engine, and is the simplest conceivable
device capable of converting heat energy into useful work.
].
The engine we have
just described is called a Carnot engine, and is the simplest conceivable
device capable of converting heat energy into useful work.
Figure 6.3:
An ideal-gas Carnot engine.
 |
For the specific case of an ideal gas, we can actually
calculate the work done per cycle, and, thereby, verify Equation (6.201).
Consider the isothermal expansion phase of the gas. For an ideal gas, the internal
energy is a function of the temperature alone. The temperature does not
change during isothermal expansion,
so the internal energy remains constant, and the net heat absorbed by the
gas must equal the work it does on the piston. Thus,
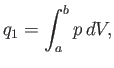 |
(6.202) |
where the expansion takes the gas from state 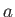 to state
to state 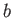 . Because
. Because
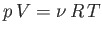 , for an ideal gas, we have
, for an ideal gas, we have
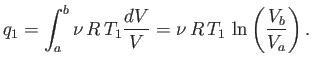 |
(6.203) |
Likewise, during the isothermal compression phase, in which
the gas goes from state  to
state
to
state 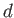 , the net heat rejected to the second reservoir
is
, the net heat rejected to the second reservoir
is
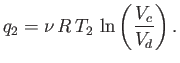 |
(6.204) |
Now, during adiabatic expansion, or compression,
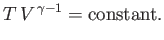 |
(6.205) |
It follows that, during the adiabatic expansion phase, which takes the gas from state
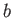 to state
to state 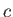 ,
,
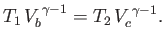 |
(6.206) |
Likewise, during the adiabatic compression phase, which takes the gas from
state 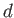 to state
to state 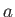 ,
,
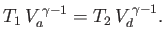 |
(6.207) |
If we take the ratio of the previous two equations then we obtain
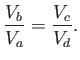 |
(6.208) |
Hence, the work done by the engine, which we can calculate using the first
law of thermodynamics,
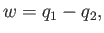 |
(6.209) |
is
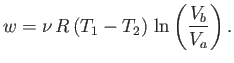 |
(6.210) |
Thus, the efficiency of the engine
is
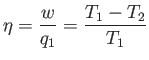 |
(6.211) |
which, not surprisingly, is identical to Equation (6.201).
The engine described previously is very idealized. Of course,
real engines are far
more complicated than this. Nevertheless, the maximum efficiency of an ideal
heat engine places severe constraints on real engines.
Conventional power stations have many different ``front ends''
(e.g., coal fired furnaces, oil fired furnaces, nuclear reactors), but their
``back ends'' are all
very similar, and consist of a steam driven turbine connected to
an electric generator. The ``front end'' heats water extracted
from a local river (say), and turns it into steam, which is then used to
drive the turbine, and, hence, to generate electricity. Finally,
the steam is sent through
a heat exchanger, so that it can heat up the incoming river water,
which means that the incoming water does not have to be heated so much by
the ``front end.''
At this stage, some heat is rejected to the environment, usually as clouds
of steam escaping from the top of cooling towers. We can see that a power station
possesses many of the same features as our idealized heat engine. There is a
cycle that operates between two temperatures. The upper temperature is the
temperature to which
the steam is heated by the ``front end,'' and the lower temperature
is the temperature of the environment into which heat is rejected. Suppose
that the steam is only heated to 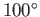 C (or 373K), and the
temperature of the environment is
C (or 373K), and the
temperature of the environment is 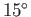 C (or 288K). It follows from
Equation (6.200) that the maximum possible efficiency of the steam cycle is
C (or 288K). It follows from
Equation (6.200) that the maximum possible efficiency of the steam cycle is
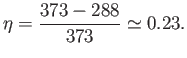 |
(6.212) |
So, at least 77% of the heat energy generated by the ``front end''
goes straight up the cooling towers. Not surprisingly, commercial
power stations do not operate with 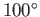 C steam. The only
way in which the thermodynamic efficiency of the steam cycle
can be raised to an acceptable level
is to use very hot steam (clearly, we cannot refrigerate the environment).
Using
C steam. The only
way in which the thermodynamic efficiency of the steam cycle
can be raised to an acceptable level
is to use very hot steam (clearly, we cannot refrigerate the environment).
Using 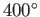 C steam, which is not uncommon, the maximum efficiency becomes
C steam, which is not uncommon, the maximum efficiency becomes
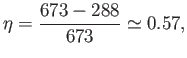 |
(6.213) |
which is more reasonable.
In fact, the steam cycles of modern power stations are so well designed that
they come surprisingly close to their
maximum thermodynamic
efficiencies.



Next: Refrigerators
Up: Classical Thermodynamics
Previous: Joule-Thompson Throttling
Richard Fitzpatrick
2016-01-25
![]() , performs a single cycle. Because
, performs a single cycle. Because
![]() has returned to its initial macrostate, its internal energy is
unchanged, and the first law of thermodynamics tell us that the work done
by the engine,
has returned to its initial macrostate, its internal energy is
unchanged, and the first law of thermodynamics tell us that the work done
by the engine, ![]() , must equal the heat extracted from the reservoir,
, must equal the heat extracted from the reservoir, ![]() , so that
, so that
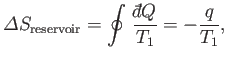
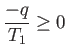
![]() ,
by extracting an amount of heat
,
by extracting an amount of heat ![]() per cycle,
without any compensating increase in the entropy of anything else, so the
second law of thermodynamics was violated. How can we remedy this situation?
We still want
the heat engine itself to perform periodic cycles (so,
by definition, its entropy cannot increase over a
cycle), and we also do not
want to increase the entropy of the external device upon which the
work is done. Our only other option is to increase the entropy of some other
body. In Carnot's analysis, this other body is
a second heat reservoir held at temperature
per cycle,
without any compensating increase in the entropy of anything else, so the
second law of thermodynamics was violated. How can we remedy this situation?
We still want
the heat engine itself to perform periodic cycles (so,
by definition, its entropy cannot increase over a
cycle), and we also do not
want to increase the entropy of the external device upon which the
work is done. Our only other option is to increase the entropy of some other
body. In Carnot's analysis, this other body is
a second heat reservoir held at temperature ![]() . We can increase the entropy
of the second reservoir by dumping some of the heat that we extracted from the
first reservoir into it. Suppose that the heat per cycle that we extract from the first
reservoir
is
. We can increase the entropy
of the second reservoir by dumping some of the heat that we extracted from the
first reservoir into it. Suppose that the heat per cycle that we extract from the first
reservoir
is ![]() , and the heat per cycle that we reject into the second reservoir
is
, and the heat per cycle that we reject into the second reservoir
is ![]() . Let the
work done on the external device be
. Let the
work done on the external device be ![]() per cycle. The first law of thermodynamics
implies that
per cycle. The first law of thermodynamics
implies that
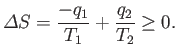
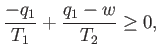
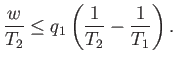
![]() and
and ![]() (where
(where ![]() ). These
reservoirs might take the form of large water baths.
Let us start off with the
gas in thermal contact with the first reservoir. We now pull the piston out,
very slowly, so that heat energy flows reversibly into the gas from the
reservoir. Let us now thermally isolate the gas, and slowly pull out
the piston some more. During this adiabatic process, the temperature of the
gas falls (because there is no longer any heat flowing into it to
compensate for the work it does on the piston). Let us continue this process
until the temperature of the gas falls to
). These
reservoirs might take the form of large water baths.
Let us start off with the
gas in thermal contact with the first reservoir. We now pull the piston out,
very slowly, so that heat energy flows reversibly into the gas from the
reservoir. Let us now thermally isolate the gas, and slowly pull out
the piston some more. During this adiabatic process, the temperature of the
gas falls (because there is no longer any heat flowing into it to
compensate for the work it does on the piston). Let us continue this process
until the temperature of the gas falls to ![]() . We now place the
gas in thermal contact with the second reservoir, and slowly push the piston
in. During this isothermal
process, heat flows out of the gas into the reservoir. We next
thermally isolate the gas a second time, and slowly compress it some more. In this
process, the temperature of the gas increases. We stop the compression when the temperature
reaches
. We now place the
gas in thermal contact with the second reservoir, and slowly push the piston
in. During this isothermal
process, heat flows out of the gas into the reservoir. We next
thermally isolate the gas a second time, and slowly compress it some more. In this
process, the temperature of the gas increases. We stop the compression when the temperature
reaches ![]() . If we carry out each step properly then we can return the gas to
its initial state, and then repeat the cycle ad infinitum.
We now have a set of reversible processes by which a quantity
of heat is extracted from the
first reservoir, and a quantity of heat is dumped into the second. We can best
evaluate
the work done by the system during each cycle
by plotting out the locus of the gas in a
. If we carry out each step properly then we can return the gas to
its initial state, and then repeat the cycle ad infinitum.
We now have a set of reversible processes by which a quantity
of heat is extracted from the
first reservoir, and a quantity of heat is dumped into the second. We can best
evaluate
the work done by the system during each cycle
by plotting out the locus of the gas in a ![]() -
-![]() diagram. The locus takes the form of a closed curve. See Figure 6.3.
The net work done per cycle is the ``area'' enclosed within this curve, because
diagram. The locus takes the form of a closed curve. See Figure 6.3.
The net work done per cycle is the ``area'' enclosed within this curve, because
![]() [if
[if ![]() is plotted vertically, and
is plotted vertically, and ![]() horizontally,
then
horizontally,
then ![]() is clearly an element of area under the curve
is clearly an element of area under the curve ![]() ].
The engine we have
just described is called a Carnot engine, and is the simplest conceivable
device capable of converting heat energy into useful work.
].
The engine we have
just described is called a Carnot engine, and is the simplest conceivable
device capable of converting heat energy into useful work.
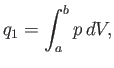
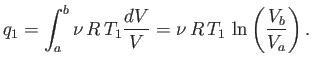
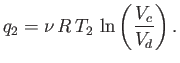
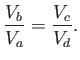
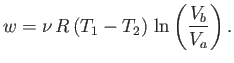
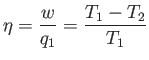
![]() C (or 373K), and the
temperature of the environment is
C (or 373K), and the
temperature of the environment is ![]() C (or 288K). It follows from
Equation (6.200) that the maximum possible efficiency of the steam cycle is
C (or 288K). It follows from
Equation (6.200) that the maximum possible efficiency of the steam cycle is