Next: Black-Body Radiation Up: Standing-Wave States Previous: Counting Standing-Wave States
 . We know
that electromagnetic radiation of angular frequency
. We know
that electromagnetic radiation of angular frequency  is quantized into photons whose energy is
is quantized into photons whose energy is
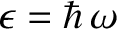 . (See Section 3.3.8 and 4.1.2.) Thus, given that photons are
indivisible, the allowed energy levels of such radiation are equally spaced, with spacing
. (See Section 3.3.8 and 4.1.2.) Thus, given that photons are
indivisible, the allowed energy levels of such radiation are equally spaced, with spacing
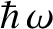 .
In this respect, each frequency state acts like a harmonic oscillator of angular frequency
.
In this respect, each frequency state acts like a harmonic oscillator of angular frequency  . (See Section 4.3.7.) According to Equation (5.390), the mean energy of a harmonic oscillator of angular frequency
. (See Section 4.3.7.) According to Equation (5.390), the mean energy of a harmonic oscillator of angular frequency
 that is in thermal equilibrium with a heat reservoir of temperature
that is in thermal equilibrium with a heat reservoir of temperature  is
Here, we have neglected the zero-point energy,
is
Here, we have neglected the zero-point energy,
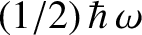 , in
Equation (5.390) because there is no electromagnetic zero-point energy.
, in
Equation (5.390) because there is no electromagnetic zero-point energy.
Let 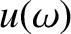 be the electromagnetic energy per unit volume associated with electromagnetic
waves whose angular frequencies lie between
be the electromagnetic energy per unit volume associated with electromagnetic
waves whose angular frequencies lie between  and
and
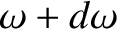 . It follows
that
. It follows
that
 |
(5.468) |
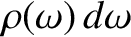 is the number of electromagnetic wave states whose angular frequencies lie between
is the number of electromagnetic wave states whose angular frequencies lie between  and
and
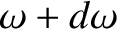 . Making use of Equations (5.457) and (5.467), we deduce that
. Making use of Equations (5.457) and (5.467), we deduce that
![$\displaystyle u(\omega) = \frac{\hbar\,\omega^3}{\pi^2\,c^3\,[\exp(\hbar\,\omega/k_B\,T)-1]}.$](img4336.png) |
(5.469) |
![\includegraphics[width=0.85\textwidth]{Chapter06/planck.eps}](img4337.png) |
Consider the classical limit
 . In this limit, the previous expression becomes
. In this limit, the previous expression becomes
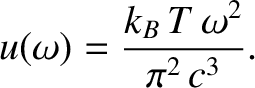 |
(5.470) |
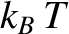 predicted by the
equipartition theorem. (See Section 5.5.5.) The total
classical energy density of electromagnetic radiation is given by
predicted by the
equipartition theorem. (See Section 5.5.5.) The total
classical energy density of electromagnetic radiation is given by
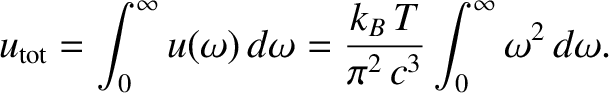 |
(5.471) |
The Planck radiation law approximates to the
classical Rayleigh-Jeans law for
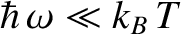 , peaks at about
, peaks at about
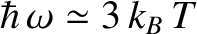 , and falls off exponentially for
, and falls off exponentially for
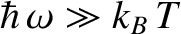 . See Figure 5.7.
The exponential fall-off at high frequencies ensures that the total energy density of electromagnetic radiation inside an enclosed cavity
remains finite. The reason for the fall-off that it is very difficult for a thermal
fluctuation to create a photon with an energy greatly in excess of
. See Figure 5.7.
The exponential fall-off at high frequencies ensures that the total energy density of electromagnetic radiation inside an enclosed cavity
remains finite. The reason for the fall-off that it is very difficult for a thermal
fluctuation to create a photon with an energy greatly in excess of 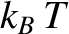 ,
because
,
because 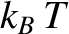 is the characteristic energy associated with such fluctuations.
is the characteristic energy associated with such fluctuations.