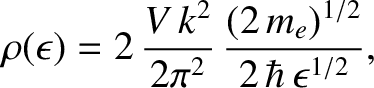Consider a three-dimensional standing wave confined in a cubic box that extends from 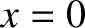 to
to  , from
, from 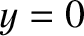 to
to 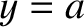 , and from
, and from 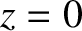 to
to 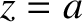 . (See Section 4.4.2.) The
wavefunction,
. (See Section 4.4.2.) The
wavefunction,
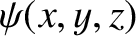 , must satisfy the boundary conditions
Thus,
standing-wave solutions of the form
, must satisfy the boundary conditions
Thus,
standing-wave solutions of the form
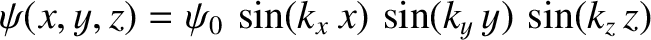 |
(5.442) |
are only acceptable if
where 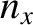 ,
, 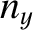 , and
, and 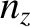 are positive integers. (Note that negative values of
are positive integers. (Note that negative values of 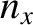 do not give rise to wave states that are physically distinct from the corresponding positive values, et cetera.) It follows that
do not give rise to wave states that are physically distinct from the corresponding positive values, et cetera.) It follows that  ,
, 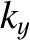 , and
, and 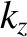 are all quantized in units of
are all quantized in units of 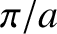 .
.
Now,
Thus, the number of translational wave states that are such that  lies between
lies between  and
and 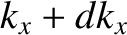 ,
,
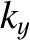 lies between
lies between 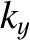 and
and  , and
, and
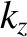 lies between
lies between 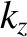 and
and 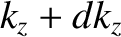 , is
, is
 |
(5.449) |
Note that
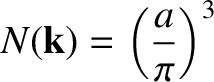 |
(5.450) |
is independent of the wavevector
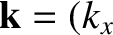 ,
, 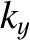 ,
, 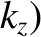 , because the allowed wave states are
uniformly distributed in
, because the allowed wave states are
uniformly distributed in  -space.
-space.
The wavenumber is defined
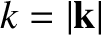 . The number of
translational wave states such that
. The number of
translational wave states such that  lies between
lies between  and
and 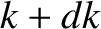 is denoted
is denoted
 , where
, where
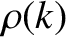 is termed the density of states. Now,
is termed the density of states. Now,
 is the number of wave states that
lie in an octant of a spherical annulus in
is the number of wave states that
lie in an octant of a spherical annulus in  -space whose inner radius is
-space whose inner radius is  , and whose outer radius is
, and whose outer radius is
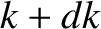 . We have to take an octant of the annulus because only wave states characterized by positive values of
. We have to take an octant of the annulus because only wave states characterized by positive values of
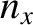 ,
, 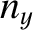 , and
, and 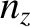 have physical significance. (See Section 4.4.3.) The volume of the octant in
have physical significance. (See Section 4.4.3.) The volume of the octant in  -space is
-space is
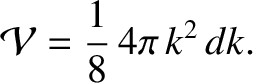 |
(5.451) |
Hence,
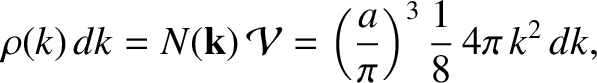 |
(5.452) |
which implies that
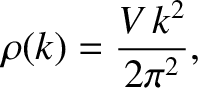 |
(5.453) |
where 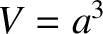 is the volume of the box. Although the previous expression was derived for the
special case of a cubic box, we shall assume that it is valid for a macroscopic box of any shape.
This assumption is reasonable provided that the wavelengths of most of the standing
waves confined in the box are much smaller than the dimensions of the box (i.e., provided that
is the volume of the box. Although the previous expression was derived for the
special case of a cubic box, we shall assume that it is valid for a macroscopic box of any shape.
This assumption is reasonable provided that the wavelengths of most of the standing
waves confined in the box are much smaller than the dimensions of the box (i.e., provided that 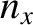 ,
, 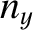 , and
, and
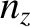 are all typically much greater than unity).
are all typically much greater than unity).
Consider electromagnetic waves confined in a box. Such waves satisfy the dispersion relation
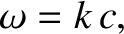 |
(5.454) |
where  is the speed of light in vacuum. (See Section 2.4.4.) Note that
is the speed of light in vacuum. (See Section 2.4.4.) Note that  is not a function of
is not a function of  . Let
. Let
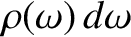 be the number of translational electromagnetic wave states for which
be the number of translational electromagnetic wave states for which  lies between
lies between  and
and
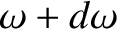 .
It follows that
.
It follows that
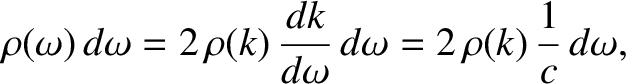 |
(5.455) |
which yields
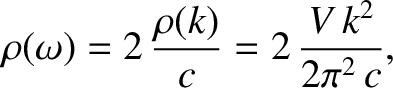 |
(5.456) |
giving
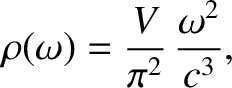 |
(5.457) |
where use has been made of Equations (5.453) and (5.454).
Here, the factor of 2 in Equation (5.455) is required because electromagnetic waves are transverse waves, so there are two independent polarization states for each allowed translational state. (See Section 2.4.4.)
Consider sound waves propagating through a solid. Such waves satisfy the dispersion relation
 |
(5.458) |
where 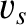 is the sound speed. Note that
is the sound speed. Note that 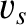 is not (usually) a function of
is not (usually) a function of  . However, solids suppose both transverse and longitudinal
sound waves (unlike gases, which only support longitudinal waves). Of course, for transverse waves, there are
two independent polarization states for each allowed translational state. However, for longitudinal waves, there is only one
polarization state for each allowed translational state. Thus, by analogy with electromagnetic waves, the
density of transverse sound wave states is
. However, solids suppose both transverse and longitudinal
sound waves (unlike gases, which only support longitudinal waves). Of course, for transverse waves, there are
two independent polarization states for each allowed translational state. However, for longitudinal waves, there is only one
polarization state for each allowed translational state. Thus, by analogy with electromagnetic waves, the
density of transverse sound wave states is
 |
(5.459) |
where 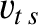 is the characteristic phase velocity of transverse waves, whereas the density of longitudinal sound wave states is
is the characteristic phase velocity of transverse waves, whereas the density of longitudinal sound wave states is
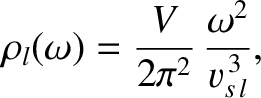 |
(5.460) |
where 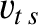 is the characteristic phase velocity of longitudinal waves. The total density of sound wave states, irrespective of the
wave polarization, is
is the characteristic phase velocity of longitudinal waves. The total density of sound wave states, irrespective of the
wave polarization, is
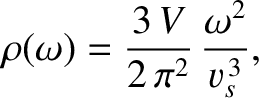 |
(5.461) |
where
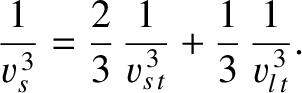 |
(5.462) |
Here, 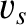 is the average sound speed.
is the average sound speed.
Finally, consider electrons of mass 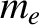 confined in a box. According to quantum mechanics, electrons have wavelike properties such that the electron energy,
confined in a box. According to quantum mechanics, electrons have wavelike properties such that the electron energy,  , is related to the wavenumber,
, is related to the wavenumber,  , according to
the dispersion relation
, according to
the dispersion relation
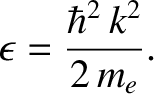 |
(5.463) |
(See Section 4.4.2.)
Let
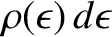 be the number of translational electron states for which
be the number of translational electron states for which  lies between
lies between  and
and
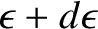 .
It follows that
.
It follows that
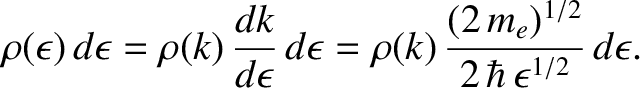 |
(5.464) |
However, according to the Pauli exclusion principle (see Section 4.4.3), only two electrons (corresponding to a spin-up
electron, and a spin-down electron) can be put into each translational state. Hence, reinterpreting
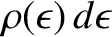 as the number of electrons whose energies lies between
as the number of electrons whose energies lies between  and
and
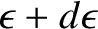 , we get
, we get
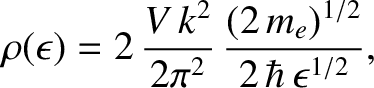 |
(5.465) |
which gives
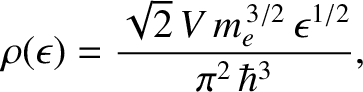 |
(5.466) |
where use has been made of Equations (5.453) and (5.463).
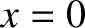 to
to  , from
, from 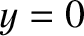 to
to 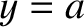 , and from
, and from 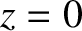 to
to 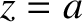 . (See Section 4.4.2.) The
wavefunction,
. (See Section 4.4.2.) The
wavefunction,
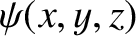 , must satisfy the boundary conditions
, must satisfy the boundary conditions
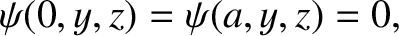
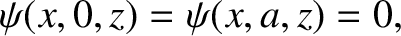
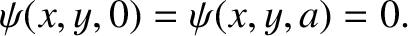
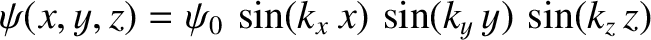

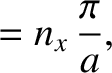
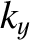
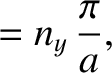
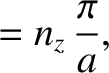
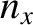 ,
, 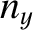 , and
, and 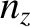 are positive integers. (Note that negative values of
are positive integers. (Note that negative values of 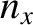 do not give rise to wave states that are physically distinct from the corresponding positive values, et cetera.) It follows that
do not give rise to wave states that are physically distinct from the corresponding positive values, et cetera.) It follows that  ,
, 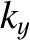 , and
, and 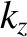 are all quantized in units of
are all quantized in units of 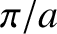 .
.
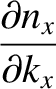
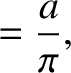
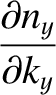
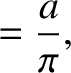
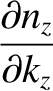
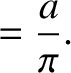
 lies between
lies between  and
and 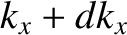 ,
,
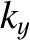 lies between
lies between 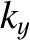 and
and  , and
, and
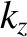 lies between
lies between 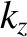 and
and 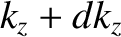 , is
, is

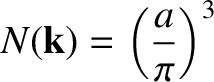
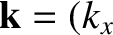 ,
, 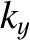 ,
, 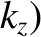 , because the allowed wave states are
uniformly distributed in
, because the allowed wave states are
uniformly distributed in  -space.
-space.
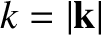 . The number of
translational wave states such that
. The number of
translational wave states such that  lies between
lies between  and
and 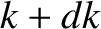 is denoted
is denoted
 , where
, where
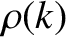 is termed the density of states. Now,
is termed the density of states. Now,
 is the number of wave states that
lie in an octant of a spherical annulus in
is the number of wave states that
lie in an octant of a spherical annulus in  -space whose inner radius is
-space whose inner radius is  , and whose outer radius is
, and whose outer radius is
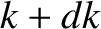 . We have to take an octant of the annulus because only wave states characterized by positive values of
. We have to take an octant of the annulus because only wave states characterized by positive values of
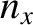 ,
, 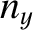 , and
, and 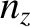 have physical significance. (See Section 4.4.3.) The volume of the octant in
have physical significance. (See Section 4.4.3.) The volume of the octant in  -space is
-space is
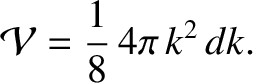
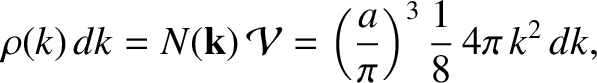
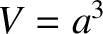 is the volume of the box. Although the previous expression was derived for the
special case of a cubic box, we shall assume that it is valid for a macroscopic box of any shape.
This assumption is reasonable provided that the wavelengths of most of the standing
waves confined in the box are much smaller than the dimensions of the box (i.e., provided that
is the volume of the box. Although the previous expression was derived for the
special case of a cubic box, we shall assume that it is valid for a macroscopic box of any shape.
This assumption is reasonable provided that the wavelengths of most of the standing
waves confined in the box are much smaller than the dimensions of the box (i.e., provided that  ,
,  , and
, and
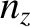 are all typically much greater than unity).
are all typically much greater than unity).
 is the speed of light in vacuum. (See Section 2.4.4.) Note that
is the speed of light in vacuum. (See Section 2.4.4.) Note that  is not a function of
is not a function of  . Let
. Let
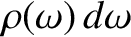 be the number of translational electromagnetic wave states for which
be the number of translational electromagnetic wave states for which  lies between
lies between  and
and
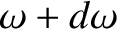 .
It follows that
which yields
giving
where use has been made of Equations (5.453) and (5.454).
Here, the factor of 2 in Equation (5.455) is required because electromagnetic waves are transverse waves, so there are two independent polarization states for each allowed translational state. (See Section 2.4.4.)
.
It follows that
which yields
giving
where use has been made of Equations (5.453) and (5.454).
Here, the factor of 2 in Equation (5.455) is required because electromagnetic waves are transverse waves, so there are two independent polarization states for each allowed translational state. (See Section 2.4.4.)

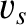 is the sound speed. Note that
is the sound speed. Note that 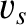 is not (usually) a function of
is not (usually) a function of  . However, solids suppose both transverse and longitudinal
sound waves (unlike gases, which only support longitudinal waves). Of course, for transverse waves, there are
two independent polarization states for each allowed translational state. However, for longitudinal waves, there is only one
polarization state for each allowed translational state. Thus, by analogy with electromagnetic waves, the
density of transverse sound wave states is
. However, solids suppose both transverse and longitudinal
sound waves (unlike gases, which only support longitudinal waves). Of course, for transverse waves, there are
two independent polarization states for each allowed translational state. However, for longitudinal waves, there is only one
polarization state for each allowed translational state. Thus, by analogy with electromagnetic waves, the
density of transverse sound wave states is

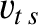 is the characteristic phase velocity of transverse waves, whereas the density of longitudinal sound wave states is
is the characteristic phase velocity of transverse waves, whereas the density of longitudinal sound wave states is
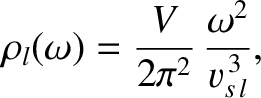
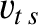 is the characteristic phase velocity of longitudinal waves. The total density of sound wave states, irrespective of the
wave polarization, is
where
is the characteristic phase velocity of longitudinal waves. The total density of sound wave states, irrespective of the
wave polarization, is
where
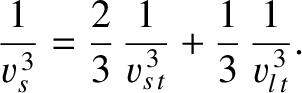
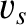 is the average sound speed.
is the average sound speed.
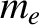 confined in a box. According to quantum mechanics, electrons have wavelike properties such that the electron energy,
confined in a box. According to quantum mechanics, electrons have wavelike properties such that the electron energy,  , is related to the wavenumber,
, is related to the wavenumber,  , according to
the dispersion relation
, according to
the dispersion relation
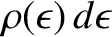 be the number of translational electron states for which
be the number of translational electron states for which  lies between
lies between  and
and
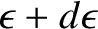 .
It follows that
.
It follows that
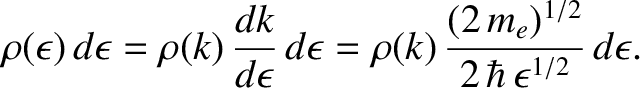
 as the number of electrons whose energies lies between
as the number of electrons whose energies lies between  and
and
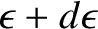 , we get
, we get