Particle in Box
As an example of a three-dimensional problem in wave mechanics, consider a particle trapped in a square potential well of infinite depth,
such that
![\begin{displaymath}U(x,y,z) = \left\{
\begin{array}{lll}
0&\mbox{\hspace{0.5cm}}...
...z\leq a\\ [0.5ex]
\infty &&\mbox{otherwise}
\end{array}\right..\end{displaymath}](img3301.png) |
(4.193) |
Within the well, the stationary wavefunction,
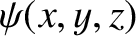 , satisfies
, satisfies
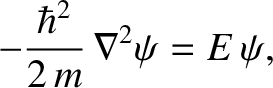 |
(4.194) |
subject to the boundary conditions
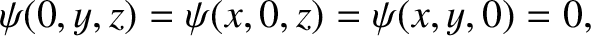 |
(4.195) |
and
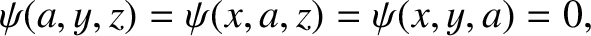 |
(4.196) |
because  outside the well.
Let us try a separable wavefunction of the form
outside the well.
Let us try a separable wavefunction of the form
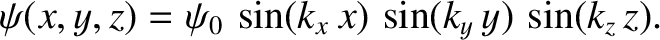 |
(4.197) |
This expression automatically satisfies the boundary conditions (4.195). The
remaining boundary conditions, (4.196), are satisfied provided
where 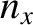 ,
, 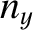 , and
, and 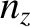 are (independent) positive integers. (Note that a negative value of
are (independent) positive integers. (Note that a negative value of 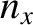 does not
give rise to a physical state that is distinct from the corresponding positive value, et cetera.)
Substitution of the wavefunction (4.197) into Equation (4.194)
yields
does not
give rise to a physical state that is distinct from the corresponding positive value, et cetera.)
Substitution of the wavefunction (4.197) into Equation (4.194)
yields
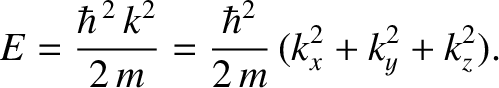 |
(4.201) |
Thus, it follows from Equations (4.198)–(4.200) that the particle energy is quantized, and that the
allowed energy levels are
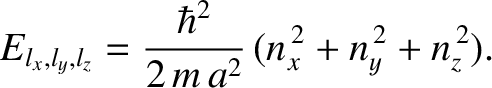 |
(4.202) |
The properly normalized [see Equation (4.187)] stationary wavefunctions corresponding to
these energy levels are
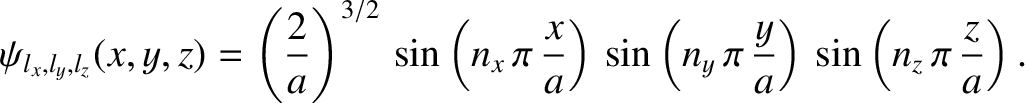 |
(4.203) |
As is the case for a particle trapped in a one-dimensional potential well, the lowest
energy level for a particle trapped in a three-dimensional well is not zero, but rather
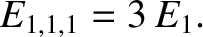 |
(4.204) |
Here,
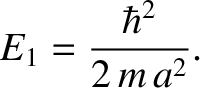 |
(4.205) |
is the ground state (i.e., the lowest energy state) energy in the one-dimensional
case.
It follows from Equation (4.202) that distinct permutations of 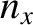 ,
, 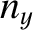 , and
, and 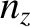 that do
not alter the value of
that do
not alter the value of
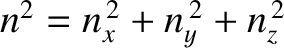 also do not alter the energy. In other words, in three dimensions,
it is possible for distinct wavefunctions to be associated with the same energy level. In this
situation, the energy level is said to be degenerate.The
ground-state energy level,
also do not alter the energy. In other words, in three dimensions,
it is possible for distinct wavefunctions to be associated with the same energy level. In this
situation, the energy level is said to be degenerate.The
ground-state energy level, 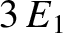 , is non-degenerate,
because the only combination of (
, is non-degenerate,
because the only combination of (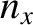 ,
, 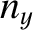 ,
, 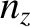 ) that gives this energy is (
) that gives this energy is ( ,
,  ,
,  ).
However, the next highest energy level,
).
However, the next highest energy level, 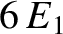 , is degenerate, because it is obtained when (
, is degenerate, because it is obtained when (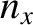 ,
, 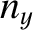 ,
, 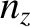 )
take the values (
)
take the values (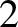 ,
,  ,
,  ),
or (
),
or ( ,
, 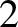 ,
,  ), or (
), or ( ,
,  ,
, 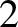 ). In fact, a non-degenerate energy
level corresponds to a case where the three quantum numbers (i.e.,
). In fact, a non-degenerate energy
level corresponds to a case where the three quantum numbers (i.e., 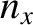 ,
, 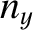 , and
, and 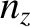 ) all have
the same value, whereas a threefold degenerate energy level corresponds to a case where only
two of the quantum numbers have the same value, and, finally, a sixfold degenerate energy level corresponds to a
case where the quantum numbers are all different.
) all have
the same value, whereas a threefold degenerate energy level corresponds to a case where only
two of the quantum numbers have the same value, and, finally, a sixfold degenerate energy level corresponds to a
case where the quantum numbers are all different.
![\begin{displaymath}U(x,y,z) = \left\{
\begin{array}{lll}
0&\mbox{\hspace{0.5cm}}...
...z\leq a\\ [0.5ex]
\infty &&\mbox{otherwise}
\end{array}\right..\end{displaymath}](img3301.png)
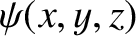 , satisfies
subject to the boundary conditions
and
because
, satisfies
subject to the boundary conditions
and
because  outside the well.
Let us try a separable wavefunction of the form
This expression automatically satisfies the boundary conditions (4.195). The
remaining boundary conditions, (4.196), are satisfied provided
where
outside the well.
Let us try a separable wavefunction of the form
This expression automatically satisfies the boundary conditions (4.195). The
remaining boundary conditions, (4.196), are satisfied provided
where 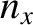 ,
, 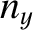 , and
, and 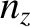 are (independent) positive integers. (Note that a negative value of
are (independent) positive integers. (Note that a negative value of 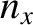 does not
give rise to a physical state that is distinct from the corresponding positive value, et cetera.)
Substitution of the wavefunction (4.197) into Equation (4.194)
yields
does not
give rise to a physical state that is distinct from the corresponding positive value, et cetera.)
Substitution of the wavefunction (4.197) into Equation (4.194)
yields
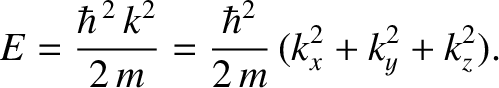
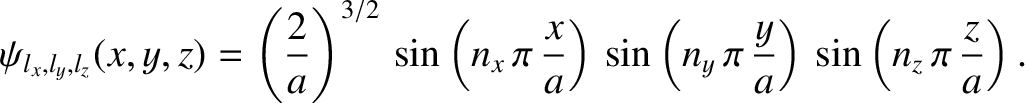
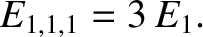
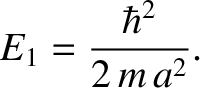
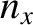 ,
, 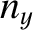 , and
, and 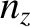 that do
not alter the value of
that do
not alter the value of
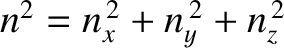 also do not alter the energy. In other words, in three dimensions,
it is possible for distinct wavefunctions to be associated with the same energy level. In this
situation, the energy level is said to be degenerate.The
ground-state energy level,
also do not alter the energy. In other words, in three dimensions,
it is possible for distinct wavefunctions to be associated with the same energy level. In this
situation, the energy level is said to be degenerate.The
ground-state energy level, 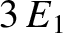 , is non-degenerate,
because the only combination of (
, is non-degenerate,
because the only combination of (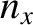 ,
, 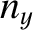 ,
, 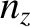 ) that gives this energy is (
) that gives this energy is ( ,
,  ,
,  ).
However, the next highest energy level,
).
However, the next highest energy level, 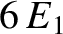 , is degenerate, because it is obtained when (
, is degenerate, because it is obtained when (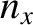 ,
, 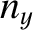 ,
, 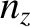 )
take the values (
)
take the values (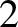 ,
,  ,
,  ),
or (
),
or ( ,
, 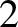 ,
,  ), or (
), or ( ,
,  ,
, 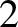 ). In fact, a non-degenerate energy
level corresponds to a case where the three quantum numbers (i.e.,
). In fact, a non-degenerate energy
level corresponds to a case where the three quantum numbers (i.e., 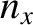 ,
, 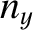 , and
, and 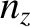 ) all have
the same value, whereas a threefold degenerate energy level corresponds to a case where only
two of the quantum numbers have the same value, and, finally, a sixfold degenerate energy level corresponds to a
case where the quantum numbers are all different.
) all have
the same value, whereas a threefold degenerate energy level corresponds to a case where only
two of the quantum numbers have the same value, and, finally, a sixfold degenerate energy level corresponds to a
case where the quantum numbers are all different.