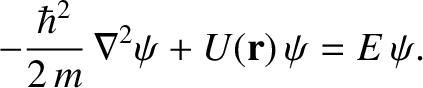Up to now, we have only discussed wave mechanics for a particle moving in one dimension. However, the
generalization to a particle moving in three dimensions is fairly straightforward.
A massive particle moving in three dimensions
has a complex wavefunction of the form [cf., Equation (4.10)]
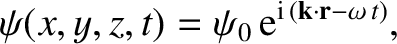 |
(4.181) |
where 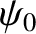 is a complex constant, and
is a complex constant, and
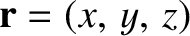 . Here, the wavevector,
. Here, the wavevector,  , and
the angular frequency,
, and
the angular frequency,  , are related to the particle momentum,
, are related to the particle momentum,  , and energy,
, and energy,  , according
to [cf., Equation (4.9)]
, according
to [cf., Equation (4.9)]
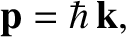 |
(4.182) |
and [cf., Equation (4.8)]
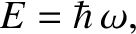 |
(4.183) |
respectively. Generalizing the
analysis of Section 4.2.2, the three-dimensional version of Schrödinger's
equation is [cf., Equation (4.22)]
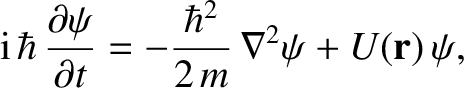 |
(4.184) |
where the differential operator
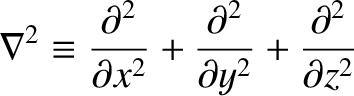 |
(4.185) |
is known as the Laplacian. (See Section A.21.) The interpretation of a three-dimensional wavefunction is that the
probability of simultaneously finding the particle between  and
and  , between
, between  and
and 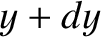 , and
between
, and
between  and
and 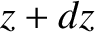 , at time
, at time  is [cf., Equation (4.25)]
is [cf., Equation (4.25)]
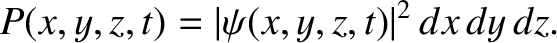 |
(4.186) |
Moreover, the normalization condition for the wavefunction becomes [cf., Equation (4.27)]
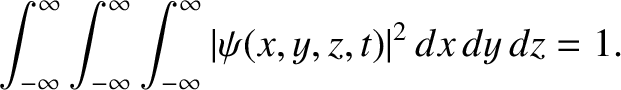 |
(4.187) |
It can be demonstrated that Schrödinger's equation, (4.184), preserves the normalization
condition, (4.187), of a localized wavefunction.
Heisenberg's uncertainty principle generalizes to [cf., Equation (4.65)]
Finally, a stationary state of energy  is written [cf., Equation (4.69)]
is written [cf., Equation (4.69)]
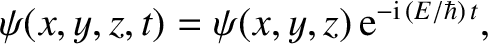 |
(4.191) |
where the stationary wavefunction,
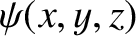 , satisfies [cf., Equation (4.71)]
, satisfies [cf., Equation (4.71)]
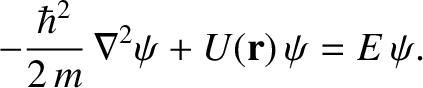 |
(4.192) |
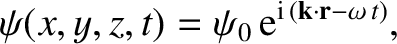
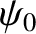 is a complex constant, and
is a complex constant, and
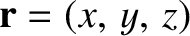 . Here, the wavevector,
. Here, the wavevector,  , and
the angular frequency,
, and
the angular frequency,  , are related to the particle momentum,
, are related to the particle momentum,  , and energy,
, and energy,  , according
to [cf., Equation (4.9)]
, according
to [cf., Equation (4.9)]
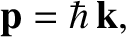
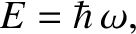
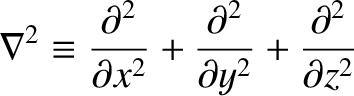
 and
and  , between
, between  and
and 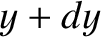 , and
between
, and
between  and
and 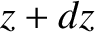 , at time
, at time  is [cf., Equation (4.25)]
is [cf., Equation (4.25)]
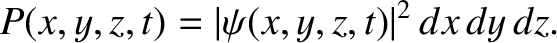
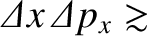
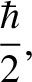

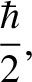
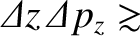
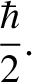
 is written [cf., Equation (4.69)]
is written [cf., Equation (4.69)]
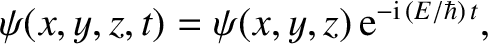
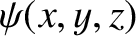 , satisfies [cf., Equation (4.71)]
, satisfies [cf., Equation (4.71)]