Wavefunctions

The basic premise of wave mechanics is that a massive particle of energy $E$ and linear momentum $p$, moving in the $x$-direction (say), can be represented by a one-dimensional wavefunction of the form

$$\psi(x,t) = \psi_0\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)},$$ (4.10)

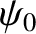where the complex amplitude, $\psi_0$, is arbitrary, while the angular frequency, $\omega$, and the wavenumber, $k$, are related to the particle energy, $E$, and momentum, $p$, via the fundamental relations

$$E = \hbar\,\omega,$$ (4.11)

$$p =\hbar\,k.$$ (4.12)

(See Section 4.1.9.)

The one-dimensional wavefunction (4.10) is the solution of a one-dimensional wave equation that determines how the wavefunction evolves in time. As described in the next section, we can guess the form of this wave equation by drawing an analogy with classical physics.