Schrödinger's Equation
A classical particle of mass  , moving in a one-dimensional potential
, moving in a one-dimensional potential 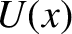 , satisfies the energy conservation
equation
, satisfies the energy conservation
equation
 |
(4.13) |
where
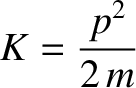 |
(4.14) |
is the particle's kinetic energy. (See Sections 1.3.2 and 1.3.5.) Hence,
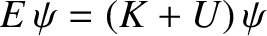 |
(4.15) |
is a valid, but not obviously useful, wave equation.
However, it follows from Equations (4.10) and (4.11) that
 |
(4.16) |
which can be rearranged to give
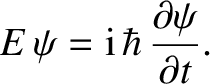 |
(4.17) |
Likewise, from Equations (4.10) and (4.12),
 |
(4.18) |
which can be rearranged to give
 |
(4.19) |
It immediately follows that
 |
(4.20) |
Hence,
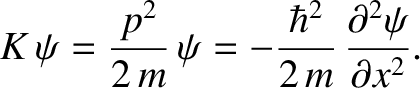 |
(4.21) |
Thus, combining Equations (4.15), (4.17), and (4.21), we obtain
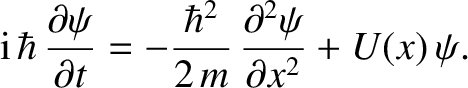 |
(4.22) |
This equation, which is known as Schrödinger's equation—because it was first formulated by Erwin Schrödinder in 1926—is the fundamental equation of wave mechanics.
For a massive particle moving in free space (i.e., 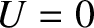 ), the complex wavefunction (4.10) is a
solution of Schrödinger's equation, (4.22), provided
), the complex wavefunction (4.10) is a
solution of Schrödinger's equation, (4.22), provided
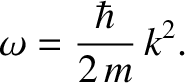 |
(4.23) |
The previous expression can be thought of as the dispersion relation for matter waves in free space. (See Section 4.2.6.) The
associated phase velocity (i.e., propagation speed of a wave maximum) is
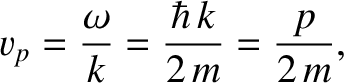 |
(4.24) |
where use has been made of Equation (4.12). However, this phase velocity is only half the classical velocity, 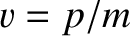 ,
of a massive (non-relativistic) particle.
,
of a massive (non-relativistic) particle.
 , moving in a one-dimensional potential
, moving in a one-dimensional potential 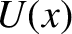 , satisfies the energy conservation
equation
, satisfies the energy conservation
equation

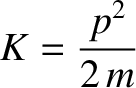




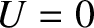 ), the complex wavefunction (4.10) is a
solution of Schrödinger's equation, (4.22), provided
), the complex wavefunction (4.10) is a
solution of Schrödinger's equation, (4.22), provided
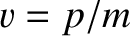 ,
of a massive (non-relativistic) particle.
,
of a massive (non-relativistic) particle.