Next: Heisenberg's Uncertainty Principle Up: Wave Mechanics Previous: Group Velocity
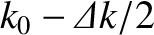 to
to
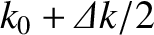 . Thus, part of the packet
propagates at the velocity
. Thus, part of the packet
propagates at the velocity
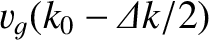 , and part at the
velocity
, and part at the
velocity
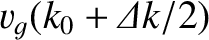 . Consequently, the packet spreads out as it propagates, because some parts of it move faster than others.
Roughly speaking, the spatial extent of the packet in real space grows as
. Consequently, the packet spreads out as it propagates, because some parts of it move faster than others.
Roughly speaking, the spatial extent of the packet in real space grows as
![$\displaystyle {\mit\Delta} x\sim ({\mit\Delta} x)_0+ \left[v_g(k_0+{\mit\Delta}...
...} k/2)\right] t\sim
({\mit\Delta} x)_0+\frac{dv_g(k_0)}{dk}\,{\mit\Delta} k\,t,$](img2995.png) |
(4.61) |
 is the extent of the packet at
is the extent of the packet at  .
Hence, from Equation (4.53),
We, thus, conclude that the spatial extent of the packet grows linearly in time, at a rate
proportional to the second derivative of
.
Hence, from Equation (4.53),
We, thus, conclude that the spatial extent of the packet grows linearly in time, at a rate
proportional to the second derivative of 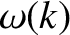 with respect to
with respect to  (evaluated at the packet's central wavenumber). This effect is
known as wave dispersion. Furthermore, it is clear that the relation
(evaluated at the packet's central wavenumber). This effect is
known as wave dispersion. Furthermore, it is clear that the relation
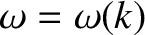 governs the degree of wave dispersion, which explains why it is called a dispersion relation.
governs the degree of wave dispersion, which explains why it is called a dispersion relation.
Note that electromagnetic wave packets, which are governed by the linear dispersion relation
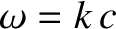 ,
do not disperse as they propagate, because
,
do not disperse as they propagate, because
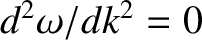 . Particle wave packets, on the other hand, are
governed by the quadratic dispersion relation (4.23) and, therefore, disperse as they propagate.
In fact, it follows from Equations (4.23) and (4.62) that the
width of a particle wave packet grows in time as
. Particle wave packets, on the other hand, are
governed by the quadratic dispersion relation (4.23) and, therefore, disperse as they propagate.
In fact, it follows from Equations (4.23) and (4.62) that the
width of a particle wave packet grows in time as
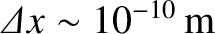 )
then the width of the packet doubles in about
)
then the width of the packet doubles in about
 .
.