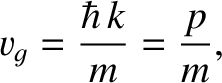Group Velocity
We have seen that Equation (4.40) is the wavefunction of a particle whose most
probable position at time  is
is 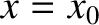 .
According to Equations (4.37) and (4.46), the wavefunction evolves in time as
.
According to Equations (4.37) and (4.46), the wavefunction evolves in time as
![$\displaystyle \psi(x,t) = \frac{1}{(2\pi)^{3/4}\,({\mit\Delta} k)^{1/2}}\int_{-...
...mega\,t-{\rm i}\,(k-k_0)\,x_0-\frac{(k-k_0)^2}{4\,({\mit\Delta k})^2}\right]dk.$](img2972.png) |
(4.50) |
Here,  is related to
is related to  via the dispersion relation (4.23); in other words,
via the dispersion relation (4.23); in other words,
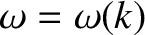 . Now, the integrand on the right-hand
side of the previous expression is strongly peaked at
. Now, the integrand on the right-hand
side of the previous expression is strongly peaked at  . It follows that the only significant contribution
to the corresponding integral comes from a small region of
. It follows that the only significant contribution
to the corresponding integral comes from a small region of  -space centered on
-space centered on  . Let us Taylor expand the
dispersion relation,
. Let us Taylor expand the
dispersion relation,
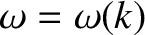 , about
, about  . Neglecting second-order terms in the expansion,
we obtain
. Neglecting second-order terms in the expansion,
we obtain
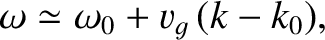 |
(4.51) |
where
Thus, we get
where
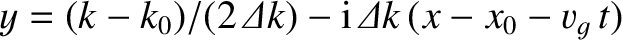 , and use has been made of Equation (4.49).
The previous equation reduces to
, and use has been made of Equation (4.49).
The previous equation reduces to
![$\displaystyle \psi(x,t) = \frac{1}{[2\pi\,({\mit\Delta} x)^2]^{1/4}}\, \exp\lef...
...,x-\omega_0\,t) - \frac{(x-x_0-v_g\,t)^{\,2}}{4\,({\mit\Delta}x)^{\,2}}\right],$](img2984.png) |
(4.55) |
where use has been made of Equations (4.43) and (4.49).
Hence, the probability of finding the particle between  and
and  at time
at time  is
is
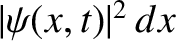 , where
, where
![$\displaystyle \vert\psi(x,t)\vert^2 = \frac{1}{[2\pi\,({\mit\Delta} x)^2]^{1/2}}\, \exp\left[- \frac{(x-x_0-v_g\,t)^{\,2}}{2\,({\mit\Delta}x)^{\,2}}\right].$](img2986.png) |
(4.56) |
It can be seen that the particle's most probable location at time  is
is
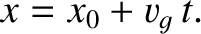 |
(4.57) |
If, as seems reasonable, we identify the velocity of the particle with the velocity of its most probable location then
we deduce that the particle effectively moves at the so-called group velocity,
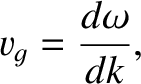 |
(4.58) |
rather than the phase velocity,
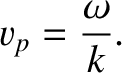 |
(4.59) |
Incidentally, the distinction between these two velocities is as follows. The phase velocity is the propagation velocity of an individual wave maximum, whereas the group velocity is the
propagation velocity of an interference peak.
We have seen that a spatially localized particle
moves at the group velocity, (4.58), rather than the phase velocity, (4.59).
Making use of the matter-wave dispersion relation, (4.23), the group velocity is
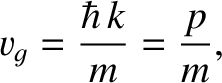 |
(4.60) |
where use has been made of Equation (4.12). This velocity is identical to the classical
velocity of a (non-relativistic) massive particle. We conclude that the matter-wave dispersion relation (4.23) is perfectly consistent
with classical physics, as long as we recognize that particles must be identified with
wave packets (which propagate at the group velocity) rather than plane waves (which propagate at the phase velocity).
 is
is 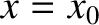 .
According to Equations (4.37) and (4.46), the wavefunction evolves in time as
.
According to Equations (4.37) and (4.46), the wavefunction evolves in time as
![$\displaystyle \psi(x,t) = \frac{1}{(2\pi)^{3/4}\,({\mit\Delta} k)^{1/2}}\int_{-...
...mega\,t-{\rm i}\,(k-k_0)\,x_0-\frac{(k-k_0)^2}{4\,({\mit\Delta k})^2}\right]dk.$](img2972.png)
 is related to
is related to  via the dispersion relation (4.23); in other words,
via the dispersion relation (4.23); in other words,
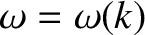 . Now, the integrand on the right-hand
side of the previous expression is strongly peaked at
. Now, the integrand on the right-hand
side of the previous expression is strongly peaked at  . It follows that the only significant contribution
to the corresponding integral comes from a small region of
. It follows that the only significant contribution
to the corresponding integral comes from a small region of  -space centered on
-space centered on  . Let us Taylor expand the
dispersion relation,
. Let us Taylor expand the
dispersion relation,
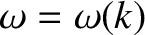 , about
, about  . Neglecting second-order terms in the expansion,
we obtain
where
. Neglecting second-order terms in the expansion,
we obtain
where
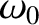
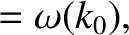
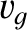
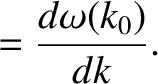
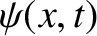
![$\displaystyle = \frac{1}{(2\pi)^{3/4}\,({\mit\Delta} k)^{1/2}}\exp[\,{\rm i}\,(...
...m i}\,(k-k_0)\,(x-x_0-v_g\,t) -\frac{(k-k_0)^2}{4\,({\mit\Delta k})^2}\right]dk$](img2981.png)
![$\displaystyle = \frac{2\,{\mit\Delta} k}{(2\pi)^{3/4}\,({\mit\Delta} k)^{1/2}}\...
...2}}{4\,({\mit\Delta}x)^{\,2}}\right]\int_{-\infty}^{\infty} {\rm e}^{-y^2}\,dy,$](img2982.png)
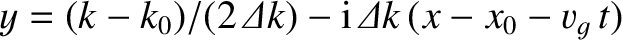 , and use has been made of Equation (4.49).
The previous equation reduces to
, and use has been made of Equation (4.49).
The previous equation reduces to
![$\displaystyle \psi(x,t) = \frac{1}{[2\pi\,({\mit\Delta} x)^2]^{1/4}}\, \exp\lef...
...,x-\omega_0\,t) - \frac{(x-x_0-v_g\,t)^{\,2}}{4\,({\mit\Delta}x)^{\,2}}\right],$](img2984.png)
 and
and  at time
at time  is
is
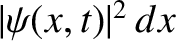 , where
It can be seen that the particle's most probable location at time
, where
It can be seen that the particle's most probable location at time  is
is