Next: Wavefunction Collapse Up: Wave Mechanics Previous: Wave Dispersion
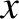 -space, with characteristic
width
-space, with characteristic
width
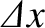 , is also localized in
, is also localized in 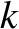 -space, with characteristic
width
-space, with characteristic
width
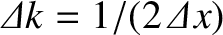 . However, as time progresses,
the width of the wave packet in
. However, as time progresses,
the width of the wave packet in 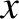 -space increases [see Equation (4.63)], while that of the packet in
-space increases [see Equation (4.63)], while that of the packet in 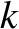 -space stays the same [because
-space stays the same [because
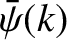 is given by Equation (4.45) at all times]. Hence,
in general, we can say that
is given by Equation (4.45) at all times]. Hence,
in general, we can say that
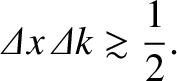 |
(4.64) |
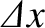 and
and
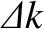 as
characterizing our uncertainty regarding the values of the particle's
position and wavenumber, respectively.
as
characterizing our uncertainty regarding the values of the particle's
position and wavenumber, respectively.
A measurement of a particle's wavenumber, 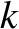 , is equivalent to
a measurement of its momentum,
, is equivalent to
a measurement of its momentum, 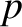 , because
, because
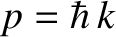 . Hence,
an uncertainty in
. Hence,
an uncertainty in 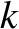 of order
of order
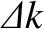 translates to
an uncertainty in
translates to
an uncertainty in 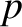 of order
of order
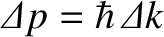 .
It follows, from the previous inequality, that
.
It follows, from the previous inequality, that
It is apparent, from Equation (4.63),
that a particle wave packet of initial spatial extent
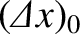 spreads out in such a manner that its spatial extent becomes
spreads out in such a manner that its spatial extent becomes
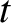 .
It is readily demonstrated that this spreading of the wave packet is a consequence of the
uncertainty principle. Indeed, because the initial uncertainty in the particle's
position is
.
It is readily demonstrated that this spreading of the wave packet is a consequence of the
uncertainty principle. Indeed, because the initial uncertainty in the particle's
position is
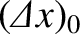 , it follows that the uncertainty in its
momentum is of order
, it follows that the uncertainty in its
momentum is of order
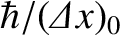 . This translates to an uncertainty
in velocity of
. This translates to an uncertainty
in velocity of
![${\mit\Delta}v = \hbar/[m\,({\mit\Delta}x)_0]$](img3011.png) . Thus,
if we imagine that part of the wave packet propagates at
. Thus,
if we imagine that part of the wave packet propagates at
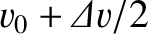 , and another part at
, and another part at
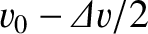 , where
, where 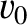 is
the mean propagation velocity, then it follows that the wave packet will
spread out as time progresses. Indeed, at large
is
the mean propagation velocity, then it follows that the wave packet will
spread out as time progresses. Indeed, at large 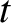 , we expect the
width of the wave packet to be
, we expect the
width of the wave packet to be
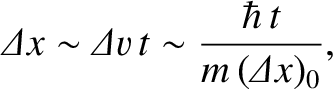 |
(4.67) |