Next: Stationary States Up: Wave Mechanics Previous: Heisenberg's Uncertainty Principle
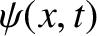 . According to our
standard interpretation,
. According to our
standard interpretation,
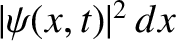 is proportional to the
probability of a measurement of the particle's position yielding
a value in the range
is proportional to the
probability of a measurement of the particle's position yielding
a value in the range  to
to  at time
at time 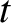 . Thus, if the wavefunction is extended then there is a wide
range of likely values that such a measurement could give.
Suppose, however, that we make a measurement of the particle's position, and obtain the value
. Thus, if the wavefunction is extended then there is a wide
range of likely values that such a measurement could give.
Suppose, however, that we make a measurement of the particle's position, and obtain the value 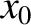 .
We now know that the particle is located at
.
We now know that the particle is located at 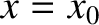 .
If we make another measurement, immediately after the first one, then
what value would we expect to obtain? Common sense tells us that
we should obtain the same value,
.
If we make another measurement, immediately after the first one, then
what value would we expect to obtain? Common sense tells us that
we should obtain the same value, 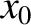 , because the particle
cannot have shifted position appreciably in an infinitesimal time interval.
Thus, immediately after the first measurement, a measurement of
the particle's position is certain to give the value
, because the particle
cannot have shifted position appreciably in an infinitesimal time interval.
Thus, immediately after the first measurement, a measurement of
the particle's position is certain to give the value 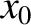 , and has
no chance of giving any other value. This implies that the
wavefunction must have collapsed to some sort of “spike” function,
centered on
, and has
no chance of giving any other value. This implies that the
wavefunction must have collapsed to some sort of “spike” function,
centered on 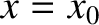 .
This idea is illustrated in Figure 4.3.
As soon as the wavefunction collapses, it starts to
expand again, as described in Section 4.2.6. Thus, the second measurement
must be made reasonably quickly after the first one, otherwise the
same result will not necessarily be obtained.
.
This idea is illustrated in Figure 4.3.
As soon as the wavefunction collapses, it starts to
expand again, as described in Section 4.2.6. Thus, the second measurement
must be made reasonably quickly after the first one, otherwise the
same result will not necessarily be obtained.
The preceding discussion illustrates an important point in wave mechanics. That is, the wavefunction of a massive particle changes discontinuously (in time) whenever a measurement of the particle's position is made. We conclude that there are two types of time evolution of the wavefunction in wave mechanics. First, there is a smooth evolution that is governed by Schrödinger's equation. This evolution takes place between measurements. Second, there is a discontinuous evolution that takes place each time a measurement is made.