Harmonic Oscillator
Our proof of the equipartition theorem depends crucially on the classical approximation. To see how
quantum effects modify this result, let us examine a particularly simple system
that we know how to analyze using both classical and quantum physics; namely,
a
simple harmonic oscillator. Consider a one-dimensional harmonic oscillator in equilibrium
with a heat reservoir held at absolute temperature  . The energy of the oscillator is given by
. The energy of the oscillator is given by
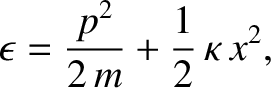 |
(5.378) |
where the first term on the right-hand side is the kinetic energy, involving the momentum,
 , and the mass,
, and the mass,  , and the second term is the potential energy, involving the displacement,
, and the second term is the potential energy, involving the displacement,
 , and the force constant,
, and the force constant, 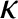 . Each of these terms is quadratic in the respective
variable. So, in the classical approximation, the equipartition theorem yields:
That is, the mean kinetic energy of the oscillator is equal
to the mean potential energy, which
equals
. Each of these terms is quadratic in the respective
variable. So, in the classical approximation, the equipartition theorem yields:
That is, the mean kinetic energy of the oscillator is equal
to the mean potential energy, which
equals
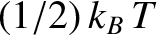 . It follows that the mean total energy is
. It follows that the mean total energy is
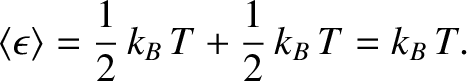 |
(5.381) |
According to quantum mechanics (see Section 4.3.7), the energy levels of a harmonic oscillator are equally
spaced, and satisfy
 |
(5.382) |
where  is a non-negative integer, and
is a non-negative integer, and
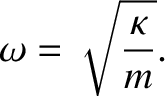 |
(5.383) |
Making use of the Boltzmann distribution, (5.329), the mean value of the quantum number  for such an oscillator is
for such an oscillator is
![$\displaystyle \langle n\rangle = \frac{\sum_{n=0,\infty}\exp[-(n+1/2)\,\hbar\,\...
...0,\infty} x^{\,n}}= x\,\frac{d}{dx}\!\left[\ln\sum_{n=0,\infty}
x^{\,n}\right],$](img4148.png) |
(5.384) |
where
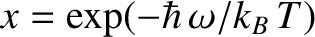 . Now,
. Now,
 |
(5.385) |
so
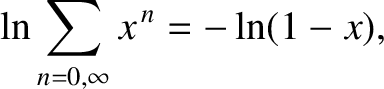 |
(5.386) |
and
![$\displaystyle x\,\frac{d}{dx}\!\left[\ln\sum_{n=0,\infty}
x^{\,n}\right]= \frac{x}{1-x}.$](img4152.png) |
(5.387) |
Hence, we deduce that
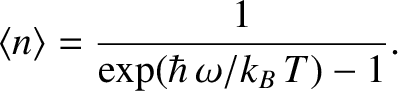 |
(5.388) |
Thus, the mean energy of the oscillator,
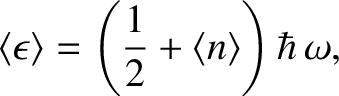 |
(5.389) |
takes the form
![$\displaystyle \langle \epsilon\rangle =\left[\frac{1}{2}+\frac{1}{\exp(\hbar\,\omega/k_B\,T)-1}\right]\hbar\,\omega.$](img4155.png) |
(5.390) |
Consider the limit
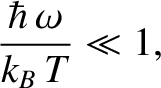 |
(5.391) |
in which the thermal energy, 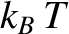 , is large compared to the separation,
, is large compared to the separation,
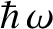 , between successive
energy levels. In this limit,
, between successive
energy levels. In this limit,
 |
(5.392) |
so
 |
(5.393) |
giving
 |
(5.394) |
Thus, the classical result, (5.381), holds whenever the thermal energy greatly exceeds the typical
spacing between quantum energy levels.
Consider the limit
 |
(5.395) |
in which the thermal energy is small compared to the separation between
the energy levels. In this limit,
 |
(5.396) |
and so
![$\displaystyle \langle \epsilon\rangle \simeq \left[\frac{1}{2}+ \exp\left(-\fra...
...omega}{k_B\,T}\right)\right]\hbar\,
\omega \simeq
\frac{1}{2} \,\hbar \,\omega.$](img4162.png) |
(5.397) |
Thus, if the thermal energy is much less than the spacing between quantum states then
the mean energy approaches that of the ground state.
Clearly, the equipartition theorem is only valid in the former limit, where
 , and the oscillator possess sufficient thermal energy to explore many
of its possible quantum states.
, and the oscillator possess sufficient thermal energy to explore many
of its possible quantum states.
 . The energy of the oscillator is given by
. The energy of the oscillator is given by
 , and the mass,
, and the mass,  , and the second term is the potential energy, involving the displacement,
, and the second term is the potential energy, involving the displacement,
 , and the force constant,
, and the force constant, 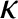 . Each of these terms is quadratic in the respective
variable. So, in the classical approximation, the equipartition theorem yields:
. Each of these terms is quadratic in the respective
variable. So, in the classical approximation, the equipartition theorem yields:
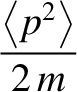
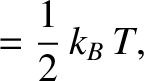
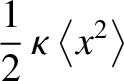

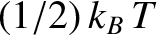 . It follows that the mean total energy is
. It follows that the mean total energy is
 is a non-negative integer, and
Making use of the Boltzmann distribution, (5.329), the mean value of the quantum number
is a non-negative integer, and
Making use of the Boltzmann distribution, (5.329), the mean value of the quantum number  for such an oscillator is
for such an oscillator is
![$\displaystyle \langle n\rangle = \frac{\sum_{n=0,\infty}\exp[-(n+1/2)\,\hbar\,\...
...0,\infty} x^{\,n}}= x\,\frac{d}{dx}\!\left[\ln\sum_{n=0,\infty}
x^{\,n}\right],$](img4148.png)
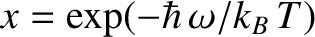 . Now,
. Now,

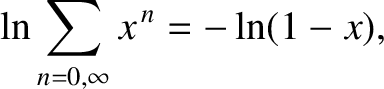
![$\displaystyle x\,\frac{d}{dx}\!\left[\ln\sum_{n=0,\infty}
x^{\,n}\right]= \frac{x}{1-x}.$](img4152.png)
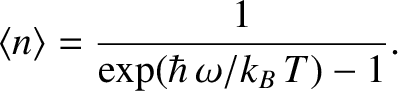
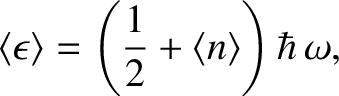
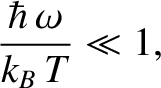
 , is large compared to the separation,
, is large compared to the separation,
 , between successive
energy levels. In this limit,
, between successive
energy levels. In this limit,
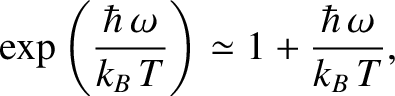

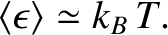
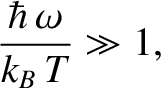

![$\displaystyle \langle \epsilon\rangle \simeq \left[\frac{1}{2}+ \exp\left(-\fra...
...omega}{k_B\,T}\right)\right]\hbar\,
\omega \simeq
\frac{1}{2} \,\hbar \,\omega.$](img4162.png)
 , and the oscillator possess sufficient thermal energy to explore many
of its possible quantum states.
, and the oscillator possess sufficient thermal energy to explore many
of its possible quantum states.