Next: Applications of Statistical Mechanics Up: Statistical Mechanics Previous: Thermodynamic Temperature
We can think of the interaction of a molecule with the
air in a classroom as
analogous to the interaction of a small system,  , in thermal contact with a
heat reservoir,
, in thermal contact with a
heat reservoir,  . The air acts like a heat reservoir because its energy
fluctuations due to interactions
with the molecule are far too small to affect any
of its macroscopic parameters. Let us
determine the probability,
. The air acts like a heat reservoir because its energy
fluctuations due to interactions
with the molecule are far too small to affect any
of its macroscopic parameters. Let us
determine the probability, 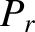 , of finding system
, of finding system  in one particular
internal state,
in one particular
internal state,  , of energy
, of energy
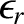 , when it is thermal equilibrium with the heat
reservoir,
, when it is thermal equilibrium with the heat
reservoir,  .
.
As usual, we assume fairly weak interaction between  and
and  , so that
the energies of these two systems
are additive. The energy of
, so that
the energies of these two systems
are additive. The energy of  is not known at this
stage. In fact, only the total internal energy of the combined system,
is not known at this
stage. In fact, only the total internal energy of the combined system,
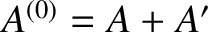 , is known. Suppose that the
total internal energy lies in the range
, is known. Suppose that the
total internal energy lies in the range 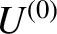 to
to
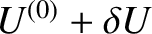 .
The overall internal energy is constant in time, because
.
The overall internal energy is constant in time, because  is assumed to be an isolated system, so
is assumed to be an isolated system, so
 |
(5.321) |
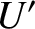 denotes the internal energy of the reservoir
denotes the internal energy of the reservoir  . Let
. Let
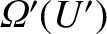 be the
number of accessible states of the reservoir when its internal energy lies in the
range
be the
number of accessible states of the reservoir when its internal energy lies in the
range 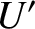 to
to
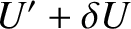 . Clearly, if system
. Clearly, if system  has an energy
has an energy
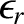 then
the reservoir
then
the reservoir  must have an energy close to
must have an energy close to
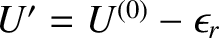 . Hence,
because
. Hence,
because  is in one definite state (i.e., state
is in one definite state (i.e., state  ), and the total
number of states accessible to
), and the total
number of states accessible to  is
is
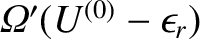 , it
follows that
the total number
of states accessible to the combined system is simply
, it
follows that
the total number
of states accessible to the combined system is simply
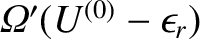 .
The principle of equal a priori probabilities tells us the probability
of occurrence of a particular situation is proportional to the number
of accessible states. Thus,
.
The principle of equal a priori probabilities tells us the probability
of occurrence of a particular situation is proportional to the number
of accessible states. Thus,
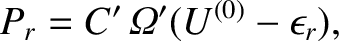 |
(5.322) |
 is a constant of proportionality that is independent of
is a constant of proportionality that is independent of  .
This constant can be determined by the normalization condition
where the sum is over all possible states of system
.
This constant can be determined by the normalization condition
where the sum is over all possible states of system  , irrespective of their energy. [See Equation (5.3).]
, irrespective of their energy. [See Equation (5.3).]
Let us now make use of the fact that system  is far smaller than system
is far smaller than system  .
It follows that
.
It follows that
 , so the slowly-varying logarithm of
, so the slowly-varying logarithm of  can be Taylor expanded about
can be Taylor expanded about
 . Thus,
. Thus,
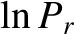 , rather than
, rather than 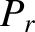 itself, because the latter
function varies so rapidly with energy
that the radius of convergence of its Taylor series
is too small for the series to be of any practical use.
The higher-order terms in Equation (5.324) can be safely
neglected, because
itself, because the latter
function varies so rapidly with energy
that the radius of convergence of its Taylor series
is too small for the series to be of any practical use.
The higher-order terms in Equation (5.324) can be safely
neglected, because
 . Now, the derivative
. Now, the derivative
![$\displaystyle \left[\frac{\partial \ln {\mit\Omega}'}{\partial U'} \right]_0 \equiv \beta$](img4018.png) |
(5.325) |
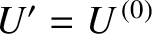 , and is, thus, a constant, independent
of the energy,
, and is, thus, a constant, independent
of the energy,
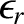 , of
, of  . In fact, we know, from the previous section, that this derivative
is just the
temperature parameter
. In fact, we know, from the previous section, that this derivative
is just the
temperature parameter
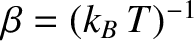 characterizing the heat
reservoir
characterizing the heat
reservoir  . Here,
. Here,  is the absolute temperature of the reservoir. Hence, Equation (5.324) becomes
is the absolute temperature of the reservoir. Hence, Equation (5.324) becomes
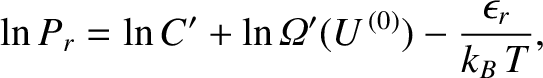 |
(5.326) |
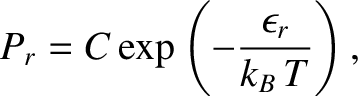 |
(5.327) |
 is a constant independent of
is a constant independent of  . The parameter
. The parameter  is determined by
the normalization condition, (5.323), which gives
is determined by
the normalization condition, (5.323), which gives
 |
(5.328) |
We conclude that the probability of a measurement of the energy of some system  , that is in thermal
equilibrium with a heat reservoir of temperature
, that is in thermal
equilibrium with a heat reservoir of temperature  , yielding the result
, yielding the result
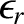 is
is