Thermodynamic Temperature
Suppose that the systems  and
and  are initially thermally isolated from one
another, with respective internal energies
are initially thermally isolated from one
another, with respective internal energies 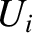 and
and 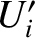 .
If the two systems are
subsequently placed in thermal contact, so that they are
free to exchange heat energy, then,
in general, the resulting state is an extremely improbable one
[i.e.,
.
If the two systems are
subsequently placed in thermal contact, so that they are
free to exchange heat energy, then,
in general, the resulting state is an extremely improbable one
[i.e., 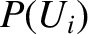 is much less than the peak probability]. The configuration will,
therefore,
tend to evolve in time until the two systems attain final energies,
is much less than the peak probability]. The configuration will,
therefore,
tend to evolve in time until the two systems attain final energies, 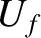 and
and 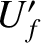 , which are such that
, which are such that  is maximized.
In the special case where the initial energies,
is maximized.
In the special case where the initial energies, 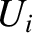 and
and 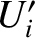 , lie very close to
the final energies,
, lie very close to
the final energies, 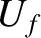 and
and 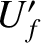 , respectively, there is no
change in the two systems when they are brought into thermal contact, because the
initial state already corresponds to a state of maximum probability.
, respectively, there is no
change in the two systems when they are brought into thermal contact, because the
initial state already corresponds to a state of maximum probability.
It follows from energy conservation that
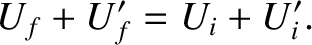 |
(5.306) |
The energy change in each system is simply the net heat absorbed, so that
The conservation of energy then reduces to
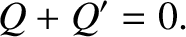 |
(5.309) |
In other words, the heat given off by one system is equal to the heat absorbed by the other.
(In our notation, absorbed
heat is positive, and emitted heat is negative.)
It is clear that if the systems  and
and  are suddenly
brought into thermal contact then they will only exchange heat, and evolve towards a
new equilibrium state, if the final state is
more probable than the initial one. In other words, the system will evolve if
are suddenly
brought into thermal contact then they will only exchange heat, and evolve towards a
new equilibrium state, if the final state is
more probable than the initial one. In other words, the system will evolve if
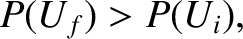 |
(5.310) |
or
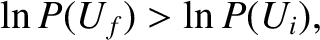 |
(5.311) |
because the logarithm is a monotonic function. The previous inequality can be written
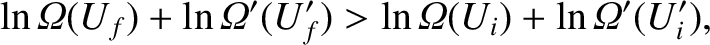 |
(5.312) |
with the aid of Equation (5.304). Taylor expansion to first order yields
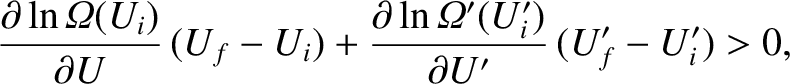 |
(5.313) |
which finally gives
![$\displaystyle [\beta(U_i) - \beta'(U_i)]\,Q >0,$](img3991.png) |
(5.314) |
where
and use has been made of Equations (5.307)–(5.309).
It is clear, from the previous analysis, that the parameter 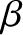 has the following properties:
has the following properties:
- If two systems separately in equilibrium have the same value of
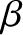 then
the systems will remain in equilibrium when brought into thermal contact with
one another.
then
the systems will remain in equilibrium when brought into thermal contact with
one another.
- If two systems separately in equilibrium have different values of
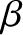 then the systems will not remain
in equilibrium when brought into thermal contact with
one another. Instead, the system with the higher value of
then the systems will not remain
in equilibrium when brought into thermal contact with
one another. Instead, the system with the higher value of 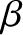 will absorb heat from the other system until the two
will absorb heat from the other system until the two 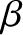 values are
the same. [See Equation (5.314).]
values are
the same. [See Equation (5.314).]
Let us define the dimensionless parameter,  , such that
, such that
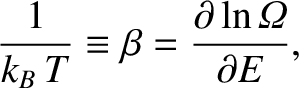 |
(5.317) |
where 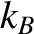 is the Boltzmann constant. The parameter
is the Boltzmann constant. The parameter  is termed the thermodynamic temperature, and controls heat flow in much the
same manner as a conventional temperature. Thus, if two isolated systems in
equilibrium possess the same thermodynamic temperature then they will remain in equilibrium
when brought into thermal contact. However,
if the two systems have different thermodynamic temperatures
then heat will flow from the system with the higher temperature
(i.e., the “hotter”
system) to the system with the lower temperature, until the temperatures of the
two systems are the same. In addition, suppose that we have three systems,
is termed the thermodynamic temperature, and controls heat flow in much the
same manner as a conventional temperature. Thus, if two isolated systems in
equilibrium possess the same thermodynamic temperature then they will remain in equilibrium
when brought into thermal contact. However,
if the two systems have different thermodynamic temperatures
then heat will flow from the system with the higher temperature
(i.e., the “hotter”
system) to the system with the lower temperature, until the temperatures of the
two systems are the same. In addition, suppose that we have three systems,  ,
,  ,
and
,
and  . We know that if
. We know that if  and
and  remain in equilibrium when brought into thermal
contact then their temperatures are the same, so that
remain in equilibrium when brought into thermal
contact then their temperatures are the same, so that  . Similarly, if
. Similarly, if
 and
and  remain in equilibrium when brought into thermal contact, then
remain in equilibrium when brought into thermal contact, then
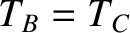 . But, we can then conclude that
. But, we can then conclude that 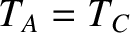 , so systems
, so systems  and
and  will also remain in equilibrium when brought into thermal contact. Thus, we arrive at
the following statement, which is sometimes called the zeroth law of
thermodynamics:
will also remain in equilibrium when brought into thermal contact. Thus, we arrive at
the following statement, which is sometimes called the zeroth law of
thermodynamics:
If two systems are separately in thermal equilibrium with a third system
then they must also be
in thermal equilibrium with one another.
Let us test our scheme out on a monatomic ideal gas. We saw in Section 5.4.4
that the number of accessible states of an ideal monatomic gas consisting of  particles is
particles is
 |
(5.318) |
where  is the internal energy,
is the internal energy,  the volume, and
the volume, and  is a constant that is independent of
is a constant that is independent of  and
and  .
According to the previous two equations, the thermodynamic temperature of such a gas is
.
According to the previous two equations, the thermodynamic temperature of such a gas is
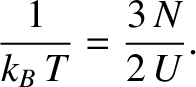 |
(5.319) |
However,
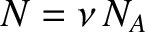 , where
, where 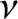 is the number of moles of molecules in the gas, and
is the number of moles of molecules in the gas, and  is
Avogadro's number. The previous equation can
be rearranged to give
is
Avogadro's number. The previous equation can
be rearranged to give
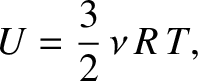 |
(5.320) |
because
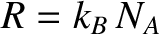 .
However, this is the correct expression for the internal energy of a monatomic ideal gas. (See Section 5.2.3.) Hence, it is clear that the thermodynamic temperature defined in Equation (5.317)
corresponds to the more familiar absolute temperature associated with an ideal gas.
.
However, this is the correct expression for the internal energy of a monatomic ideal gas. (See Section 5.2.3.) Hence, it is clear that the thermodynamic temperature defined in Equation (5.317)
corresponds to the more familiar absolute temperature associated with an ideal gas.
 and
and  are initially thermally isolated from one
another, with respective internal energies
are initially thermally isolated from one
another, with respective internal energies 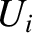 and
and 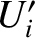 .
If the two systems are
subsequently placed in thermal contact, so that they are
free to exchange heat energy, then,
in general, the resulting state is an extremely improbable one
[i.e.,
.
If the two systems are
subsequently placed in thermal contact, so that they are
free to exchange heat energy, then,
in general, the resulting state is an extremely improbable one
[i.e., 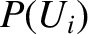 is much less than the peak probability]. The configuration will,
therefore,
tend to evolve in time until the two systems attain final energies,
is much less than the peak probability]. The configuration will,
therefore,
tend to evolve in time until the two systems attain final energies, 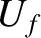 and
and 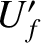 , which are such that
, which are such that  is maximized.
In the special case where the initial energies,
is maximized.
In the special case where the initial energies, 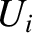 and
and 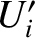 , lie very close to
the final energies,
, lie very close to
the final energies, 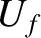 and
and 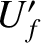 , respectively, there is no
change in the two systems when they are brought into thermal contact, because the
initial state already corresponds to a state of maximum probability.
, respectively, there is no
change in the two systems when they are brought into thermal contact, because the
initial state already corresponds to a state of maximum probability.
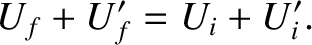
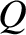
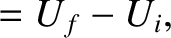
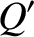

 and
and  are suddenly
brought into thermal contact then they will only exchange heat, and evolve towards a
new equilibrium state, if the final state is
more probable than the initial one. In other words, the system will evolve if
are suddenly
brought into thermal contact then they will only exchange heat, and evolve towards a
new equilibrium state, if the final state is
more probable than the initial one. In other words, the system will evolve if
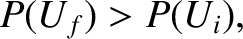
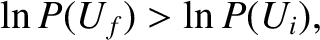
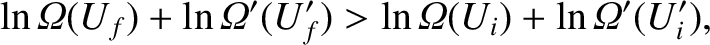
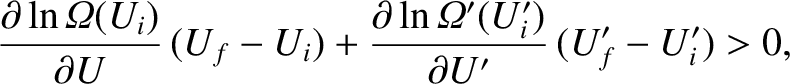
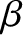

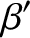
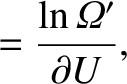
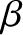 has the following properties:
has the following properties:
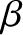 then
the systems will remain in equilibrium when brought into thermal contact with
one another.
then
the systems will remain in equilibrium when brought into thermal contact with
one another.
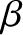 then the systems will not remain
in equilibrium when brought into thermal contact with
one another. Instead, the system with the higher value of
then the systems will not remain
in equilibrium when brought into thermal contact with
one another. Instead, the system with the higher value of 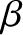 will absorb heat from the other system until the two
will absorb heat from the other system until the two 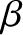 values are
the same. [See Equation (5.314).]
values are
the same. [See Equation (5.314).]
 , such that
, such that
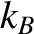 is the Boltzmann constant. The parameter
is the Boltzmann constant. The parameter  is termed the thermodynamic temperature, and controls heat flow in much the
same manner as a conventional temperature. Thus, if two isolated systems in
equilibrium possess the same thermodynamic temperature then they will remain in equilibrium
when brought into thermal contact. However,
if the two systems have different thermodynamic temperatures
then heat will flow from the system with the higher temperature
(i.e., the “hotter”
system) to the system with the lower temperature, until the temperatures of the
two systems are the same. In addition, suppose that we have three systems,
is termed the thermodynamic temperature, and controls heat flow in much the
same manner as a conventional temperature. Thus, if two isolated systems in
equilibrium possess the same thermodynamic temperature then they will remain in equilibrium
when brought into thermal contact. However,
if the two systems have different thermodynamic temperatures
then heat will flow from the system with the higher temperature
(i.e., the “hotter”
system) to the system with the lower temperature, until the temperatures of the
two systems are the same. In addition, suppose that we have three systems,  ,
,  ,
and
,
and  . We know that if
. We know that if  and
and  remain in equilibrium when brought into thermal
contact then their temperatures are the same, so that
remain in equilibrium when brought into thermal
contact then their temperatures are the same, so that  . Similarly, if
. Similarly, if
 and
and  remain in equilibrium when brought into thermal contact, then
remain in equilibrium when brought into thermal contact, then
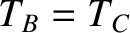 . But, we can then conclude that
. But, we can then conclude that 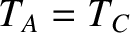 , so systems
, so systems  and
and  will also remain in equilibrium when brought into thermal contact. Thus, we arrive at
the following statement, which is sometimes called the zeroth law of
thermodynamics:
will also remain in equilibrium when brought into thermal contact. Thus, we arrive at
the following statement, which is sometimes called the zeroth law of
thermodynamics:
 particles is
particles is

 is the internal energy,
is the internal energy,  the volume, and
the volume, and  is a constant that is independent of
is a constant that is independent of  and
and  .
According to the previous two equations, the thermodynamic temperature of such a gas is
.
According to the previous two equations, the thermodynamic temperature of such a gas is
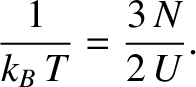
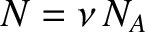 , where
, where 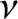 is the number of moles of molecules in the gas, and
is the number of moles of molecules in the gas, and  is
Avogadro's number. The previous equation can
be rearranged to give
is
Avogadro's number. The previous equation can
be rearranged to give
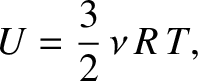
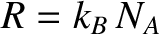 .
However, this is the correct expression for the internal energy of a monatomic ideal gas. (See Section 5.2.3.) Hence, it is clear that the thermodynamic temperature defined in Equation (5.317)
corresponds to the more familiar absolute temperature associated with an ideal gas.
.
However, this is the correct expression for the internal energy of a monatomic ideal gas. (See Section 5.2.3.) Hence, it is clear that the thermodynamic temperature defined in Equation (5.317)
corresponds to the more familiar absolute temperature associated with an ideal gas.