Next: Thermodynamic Temperature Up: Statistical Mechanics Previous: Number of Accessible States
 and
and  , that contain a large number of particles. Suppose that the internal energies of
these two systems are
, that contain a large number of particles. Suppose that the internal energies of
these two systems are  and
and 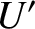 , respectively. The external parameters are held
fixed, so that systems
, respectively. The external parameters are held
fixed, so that systems  and
and  cannot do work on one another. However, we shall
assume that
the systems are free to exchange heat energy (i.e., they are in thermal contact).
It is convenient to divide the energy
scale into small subdivisions of width
cannot do work on one another. However, we shall
assume that
the systems are free to exchange heat energy (i.e., they are in thermal contact).
It is convenient to divide the energy
scale into small subdivisions of width 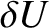 .
The number of accessible states of
.
The number of accessible states of  (i.e., states in which the internal energy of the whole
system lies between
(i.e., states in which the internal energy of the whole
system lies between  and
and
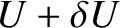 ) is denoted
) is denoted
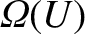 . Likewise, the number of accessible states of
. Likewise, the number of accessible states of  is
denoted
is
denoted
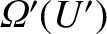 .
.
The combined system
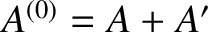 is assumed to be
isolated (i.e., it neither does work on,
nor exchanges heat with, its surroundings). It follows the total internal energy,
is assumed to be
isolated (i.e., it neither does work on,
nor exchanges heat with, its surroundings). It follows the total internal energy, 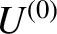 , is constant.
When
speaking of thermal contact between two distinct
systems, we usually assume that the mutual interaction is
sufficiently weak for the internal energies to be additive. Thus,
, is constant.
When
speaking of thermal contact between two distinct
systems, we usually assume that the mutual interaction is
sufficiently weak for the internal energies to be additive. Thus,
According to Equation (5.302), if the internal energy of  lies in the range
lies in the range  to
to
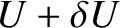 then the internal energy of
then the internal energy of  must lie between
must lie between
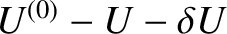 and
and
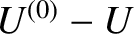 .
Thus, the number of accessible states for each system is
given by
.
Thus, the number of accessible states for each system is
given by
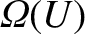 and
and
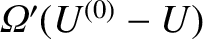 , respectively.
Because every possible state of
, respectively.
Because every possible state of  can be
combined with every possible state of
can be
combined with every possible state of  to form a distinct state,
the total number of distinct states
accessible to
to form a distinct state,
the total number of distinct states
accessible to  when the energy of
when the energy of  lies in the range
lies in the range  to
to
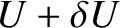 is
is
Consider an ensemble of pairs of thermally interacting systems,
 and
and  , that are left undisturbed, so that they can attain thermal equilibrium.
The principle of equal a priori probabilities is applicable to
this situation. (See Section 5.4.2.)
According to this principle, the probability of occurrence of a given macroscopic state
is proportional to the number of accessible microscopic states, because all microscopic states are
equally likely. Thus, the probability that the system
, that are left undisturbed, so that they can attain thermal equilibrium.
The principle of equal a priori probabilities is applicable to
this situation. (See Section 5.4.2.)
According to this principle, the probability of occurrence of a given macroscopic state
is proportional to the number of accessible microscopic states, because all microscopic states are
equally likely. Thus, the probability that the system  has an energy lying in
the range
has an energy lying in
the range  to
to
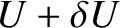 can be written
can be written
 is a constant that is independent of
is a constant that is independent of  .
.
We know, from Section 5.4.4, that the typical variation of the number of accessible states with energy is of the form
where is the number of molecules. For a macroscopic system,
is the number of molecules. For a macroscopic system,  is
an exceedingly large number. It follows that the probability,
is
an exceedingly large number. It follows that the probability,
 , in Equation (5.304) is the product
of an extremely rapidly increasing function of
, in Equation (5.304) is the product
of an extremely rapidly increasing function of  ,
and an extremely rapidly decreasing
function of
,
and an extremely rapidly decreasing
function of  . Hence, we would expect the probability
to exhibit a very pronounced
maximum at some particular value of the energy,
. Hence, we would expect the probability
to exhibit a very pronounced
maximum at some particular value of the energy, 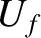 .
.