Next: Probability Calculations Up: Statistical Mechanics Previous: Specification of State of
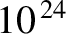 particles.
We cannot evolve
particles.
We cannot evolve 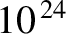 simultaneous differential equations. Even if we
could, we would not want to. After all, we are not particularly
interested in the motions of
individual
particles. What we really require is statistical information regarding the
motions of all particles in the system.
simultaneous differential equations. Even if we
could, we would not want to. After all, we are not particularly
interested in the motions of
individual
particles. What we really require is statistical information regarding the
motions of all particles in the system.
Clearly, what is needed here is a statistical treatment of the problem. Instead of focusing on a single system, let us proceed, in the usual manner, and consider a statistical ensemble consisting of a large number of identical systems. (See Section 5.1.1.) In general, these systems are distributed over many different states at any given time. In order to evaluate the probability that the system possesses a particular property, we merely need to find the number of systems in the ensemble that exhibit this property, and then divide by the total number of systems, in the limit as the latter number tends to infinity.
We can usually place some general constraints on the system.
Typically, we know the total internal energy, 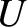 , the total volume,
, the total volume, 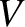 , and the
total number of particles,
, and the
total number of particles, 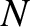 . To be more exact, we can only
really say that the total internal energy lies between
. To be more exact, we can only
really say that the total internal energy lies between 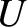 and
and
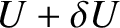 , et cetera, where
, et cetera, where
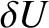 is an experimental error. Thus, we need only concern ourselves with
those systems in the ensemble exhibiting states that are consistent with the
known constraints. We shall call these the states accessible to the system.
In general, there are a great many such states.
is an experimental error. Thus, we need only concern ourselves with
those systems in the ensemble exhibiting states that are consistent with the
known constraints. We shall call these the states accessible to the system.
In general, there are a great many such states.
We now need to calculate the probability of the system being found in each of its accessible states. In fact, the only way that we could calculate these probabilities would be to evolve all of the systems in the ensemble in time, and observe how long, on average, they spend in each accessible state. But, as we have already discussed, such a calculation is completely out of the question. Instead, we shall effectively guess the probabilities.
Let us consider an isolated system in equilibrium. In this situation,
we would expect
the probability of the system being found in one of its accessible
states to be independent of time. This implies that the statistical ensemble
does not
evolve with time. Individual systems in the ensemble will constantly
change state, but the
average number of systems in any given state should remain constant. Thus, all
macroscopic parameters describing the system, such as the internal energy
and the volume, should also remain constant. There is nothing in the laws of
mechanics that would lead us to suppose that the system will be found more
often in one of its accessible states than in another. We assume,
therefore, that the system is equally likely to be found in any of
its accessible states. This assumption is called the principle of equal
a priori probabilities, and lies at the heart of statistical mechanics.
In fact, we use assumptions like this all of the time without really thinking
about them. Suppose that we were asked to pick a card at random from a well-shuffled pack of ordinary playing cards. Most people would accept that we have
an equal probability of picking any card in the pack. There is nothing that
would favor one particular card over all of the others. Hence, because there are fifty-two cards in
a normal pack, we would expect the probability of picking the ace of spades, say, to
be 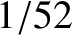 . We could now place some constraints on the system.
For instance, we could only count red cards, in which case the probability
of picking the ace of hearts, say, would be
. We could now place some constraints on the system.
For instance, we could only count red cards, in which case the probability
of picking the ace of hearts, say, would be 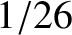 , by the same
reasoning. In both cases, we have used the principle of equal a priori
probabilities. In statistical mechanics, we treat a many-particle system a little like an
extremely
large pack of cards. Each accessible state corresponds to one of the
cards in the pack. The interactions between particles cause the system to
continually change state. This is equivalent to constantly shuffling the
pack. Finally, an observation of the state of the system is like picking
a card at random from the pack. The principle of equal a priori
probabilities then boils down to saying that we have an equal chance of
choosing any particular card.
, by the same
reasoning. In both cases, we have used the principle of equal a priori
probabilities. In statistical mechanics, we treat a many-particle system a little like an
extremely
large pack of cards. Each accessible state corresponds to one of the
cards in the pack. The interactions between particles cause the system to
continually change state. This is equivalent to constantly shuffling the
pack. Finally, an observation of the state of the system is like picking
a card at random from the pack. The principle of equal a priori
probabilities then boils down to saying that we have an equal chance of
choosing any particular card.