Next: Number of Accessible States Up: Statistical Mechanics Previous: Principle of Equal A
 to
to
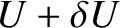 . In order to make statistical predictions, we focus attention
on an ensemble of such systems, all of which have their internal energy in this range.
Let
. In order to make statistical predictions, we focus attention
on an ensemble of such systems, all of which have their internal energy in this range.
Let
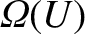 be the total number of different states in the ensemble with
internal energies in the specified range. Suppose that, among these states, there are
a number
be the total number of different states in the ensemble with
internal energies in the specified range. Suppose that, among these states, there are
a number
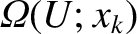 for which some parameter,
for which some parameter,  , of the system
assumes the discrete value
, of the system
assumes the discrete value 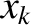 . (This discussion can easily
be generalized to deal with a parameter that can assume a continuous range of
values.) The principle of equal a priori probabilities tells us
that all of the
. (This discussion can easily
be generalized to deal with a parameter that can assume a continuous range of
values.) The principle of equal a priori probabilities tells us
that all of the
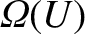 accessible states of the system are equally likely
to occur in the ensemble. It follows that the probability,
accessible states of the system are equally likely
to occur in the ensemble. It follows that the probability, 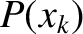 , that the
parameter
, that the
parameter  of the system assumes the value
of the system assumes the value 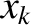 is simply
is simply
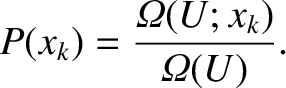 |
(5.291) |
 for the system is given by
for the system is given by
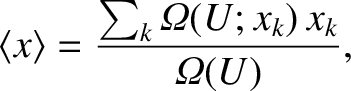 |
(5.292) |
 can assume.
can assume.